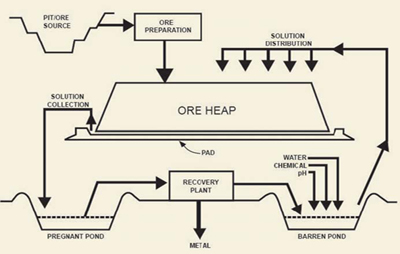
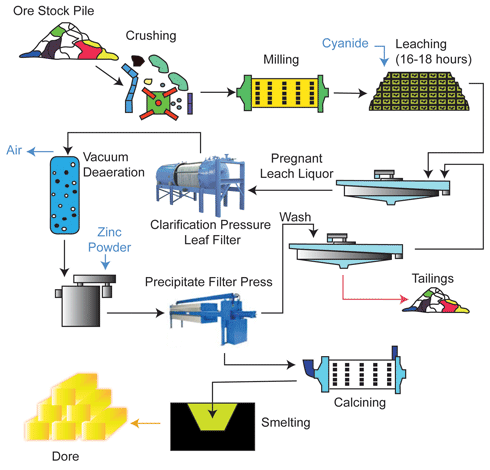
Contents Hydrometallurgical Processing Milling Leaching Metal (Quantity – % Recovery) Removal of Metal from Pulp Purification (Quality – g/L and removing other ions) Electrowinning or Precipitation Followed by Smelting Why Leaching? Traditional methods viz – ore sieving, washing, etc. are obsolete and uneconomical. Pyro-metallurgy is highly costly and non-viable […]
AMIT F145
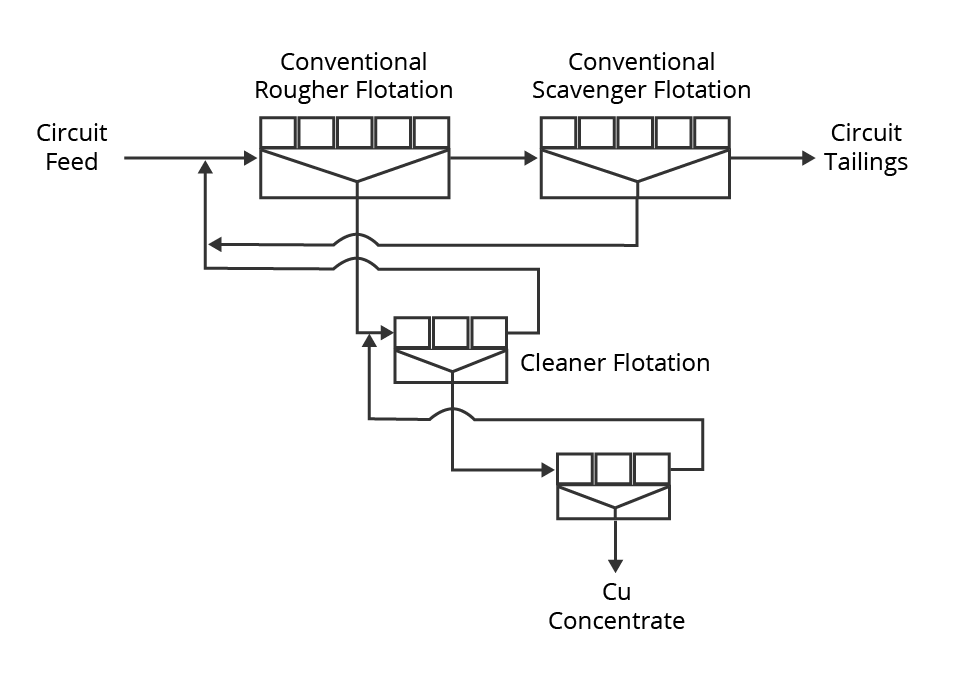
Conventional Flotation First developed in 1912. Employed throughout the 20th century. Low capital cost. Due to mixing, several cells are used in series. Hydraulic entrainment has always caused a battle between grade and recovery. 10 tph/cell capacity Microcel Bubble Generation Gold Flotation Circuit
Contents Reading DM Vessels Utilizes a suspension of magnetite to adjust the medium density to a value that is between coal and the ash bearing material. The medium density correlates to the required separation density needed to achieve a desired product grade. Feed to a heavy media vessel is injected […]
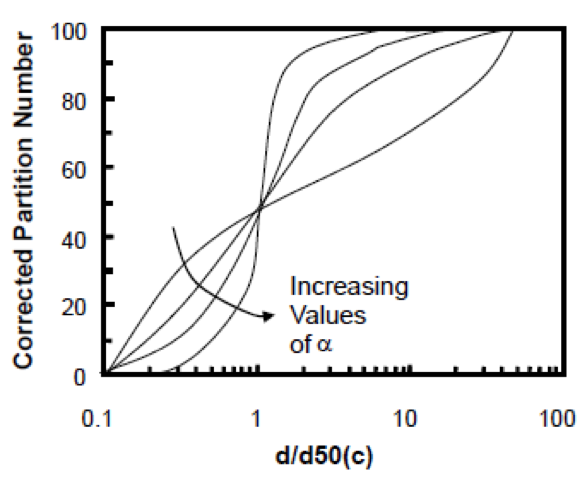
Contents Reading Classifying cyclones are the most commonly used technology for achieving particle size separations below 300 microns. Classifying cyclones are comprised of a cylindrical section and a conical section. The length of the conical section has been found to significantly effect particle size separations D50(c) Versus Overflow Size […]
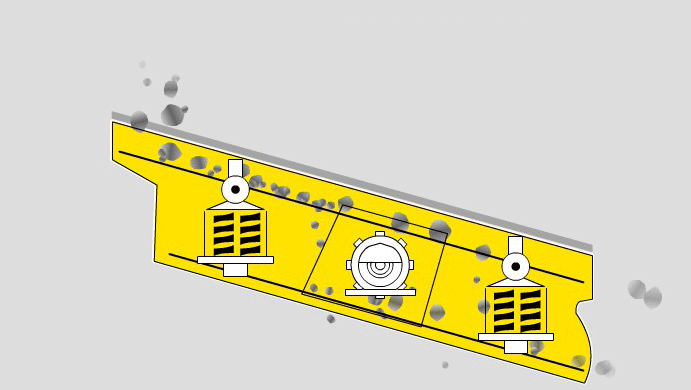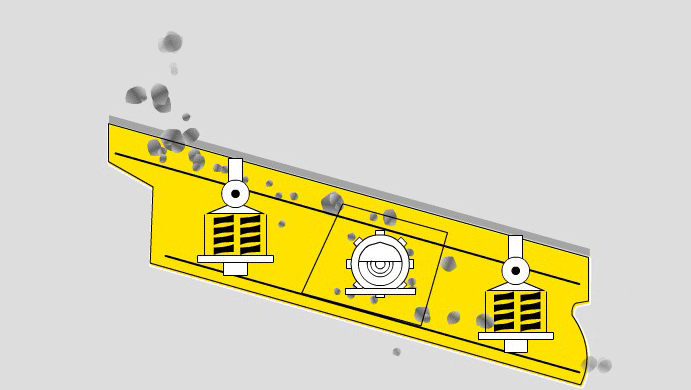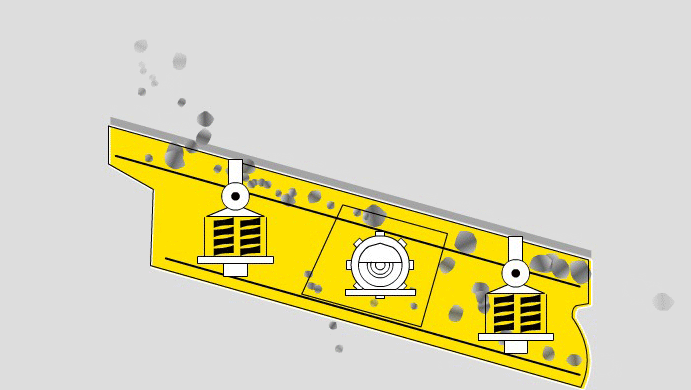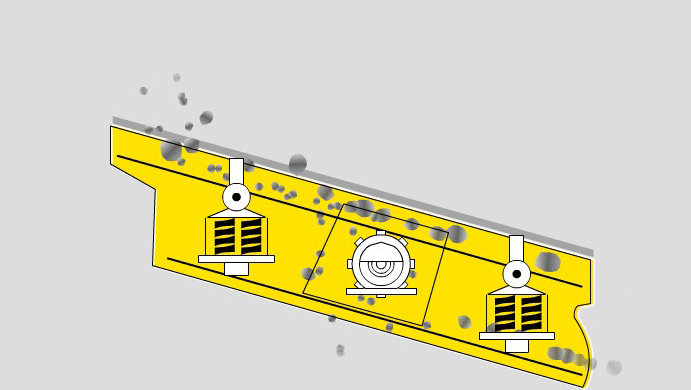
Contents Reading Industrial Screens A 20 ° inclined screen is typically used for pre screening and sizing applications. Decreasing the inclination slows the movement across the table thereby decreasing capacity but improving efficiency. Above 12 mm, dry screening is preferred. Below 12 mm, wet screening using a low-pressure water […]
COURSE INFORMATION Title: Introduction to Mineral Beneficiation Department/Number: AMIT 145 Credits: 3 Prerequisites: N/A Location: Fairbanks Pipeline Training Center (FPTC) Room #2 INSTRUCTOR INFORMATION Name: Tathagata Ghosh, Brian Ellingson COURSE READINGS/MATERIALS Course Textbook: Wills’ Mineral Processing Technology, 8th edition, B.A Wills, James Finch PhD, Butterworth-Heinemann publisher, 2015 ISBN-13: 978-0080970530 Supplementary […]
This course provides an overview or introduction into the field of mineral beneficiation and comminution, systems and equipment used for the mineral processing industry. Fundamentals of basic separation and mineral beneficiation, environmental concerns, safety and terminology will be explored. Course Information Credits: 3 Prerequisites: Placement in Mill Operations […]