Contents Objectives At the end of this lesson students should be able to: Explain the use of rod mills in mineral industry. Explain rod mill operation. Recognize different design parameters of rod mills. Explain problems associated with rod milling. Summarize considerations in rod mill selection Reading & Lecture Introduction […]
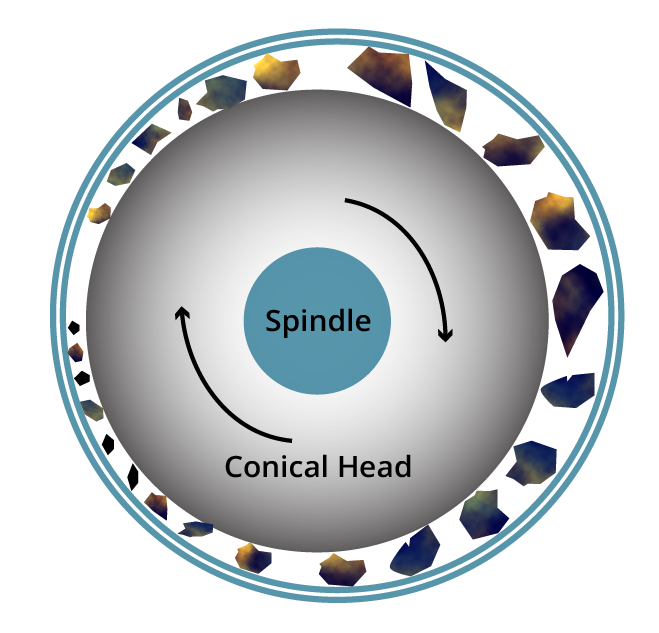
AMIT F135
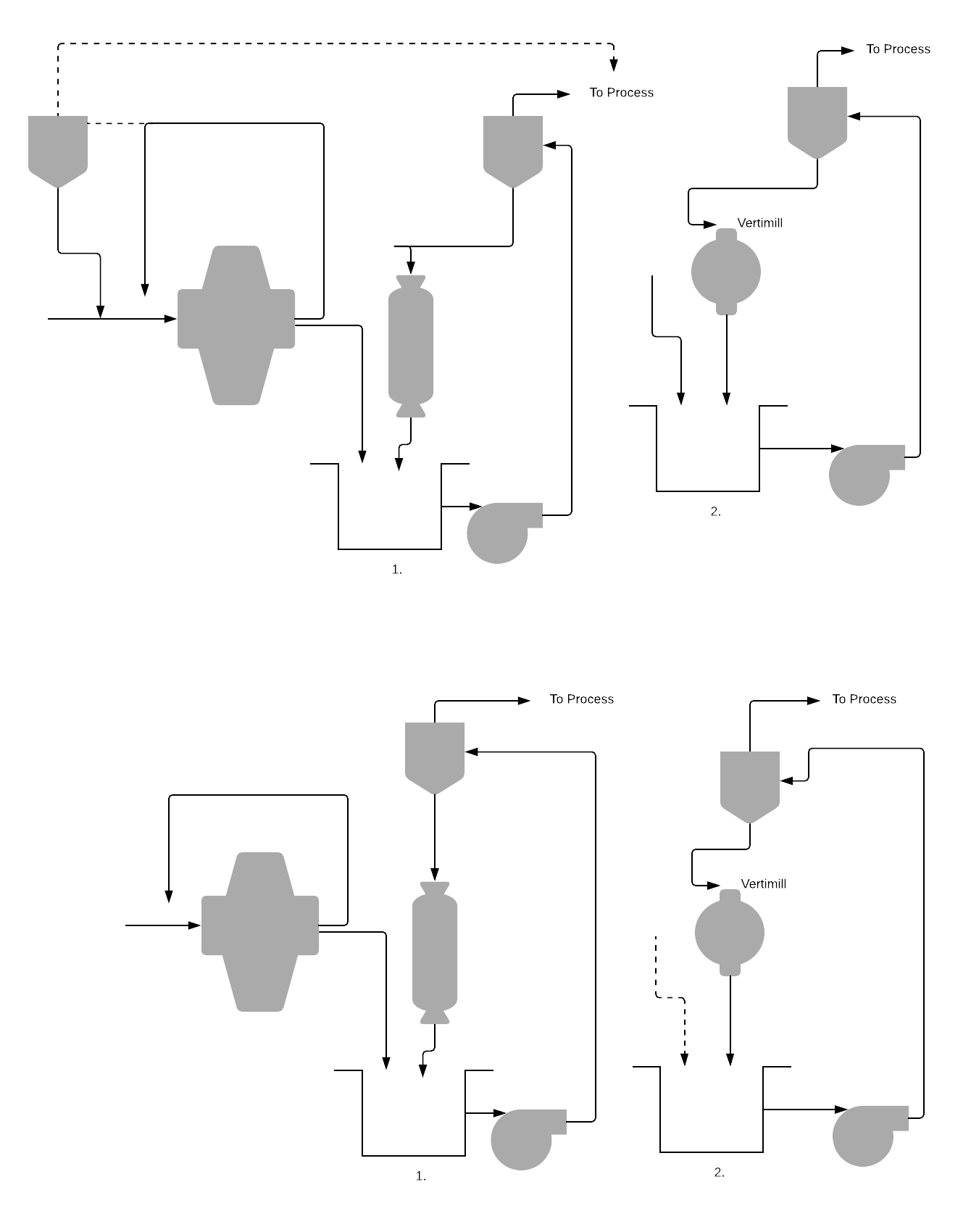
Contents Objectives At the end of this lesson students should be able to: Explain the role of ball mill in mineral industry and why it is extensively used. Describe different types of ball mill design. Describe the components of ball mill. Explain their understanding of ball mill operation. Explain the […]
Contents Objectives At the end of this lesson students should be able to: Explain the grinding process Distinguish between crushing and grinding Compare and contrast different type of equipment and their components used for grinding Identify key variables for process control Design features of grinding equipment (SAG, BALL and ROD […]
Contents Objectives At the end of this less students should be able to: Explain the need for crushing operation Define terminologies involved in crushing operation Explain how crushing works Explain the stages involved in crushing operation (Primary, Secondary and Tertiary) Recognize different types of crushing equipment used in Mineral industry […]
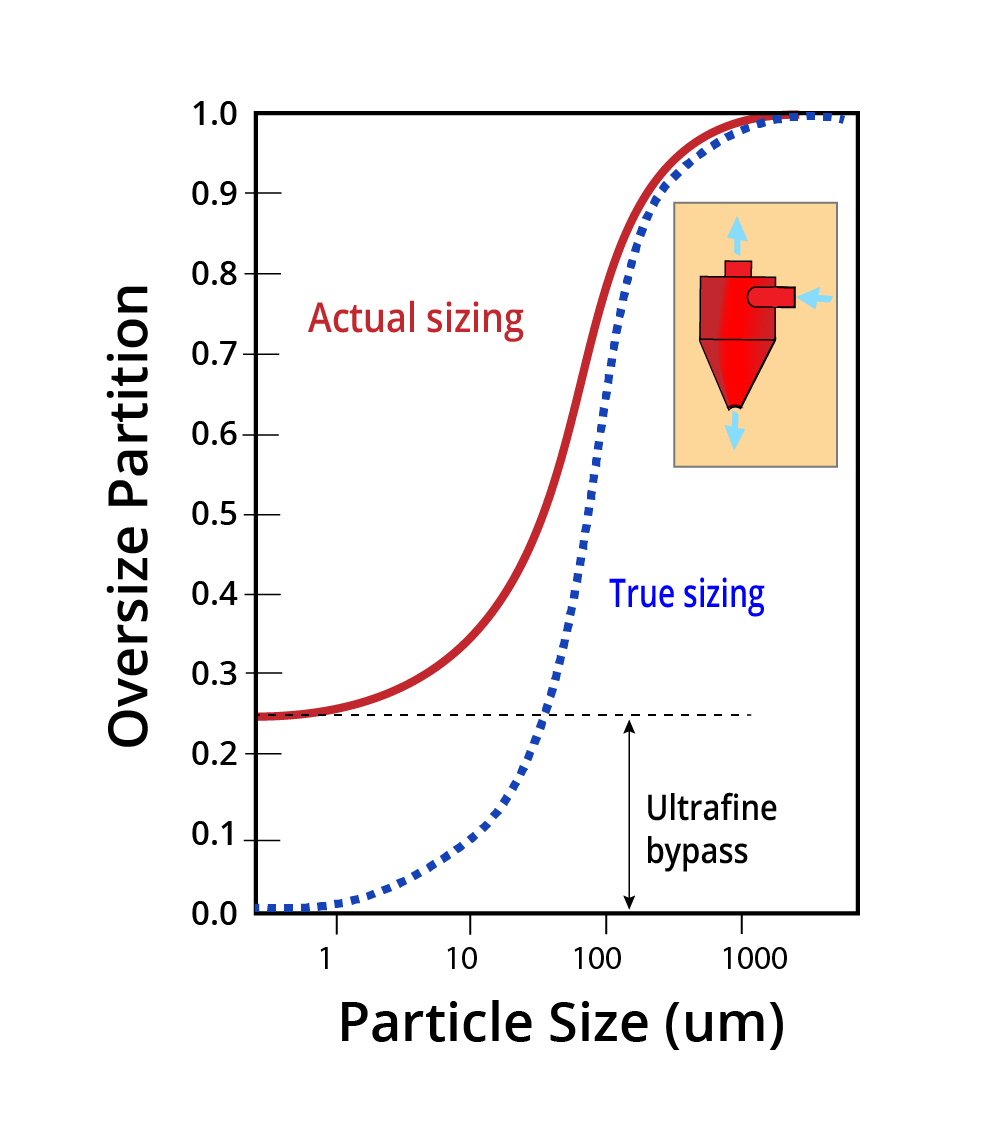
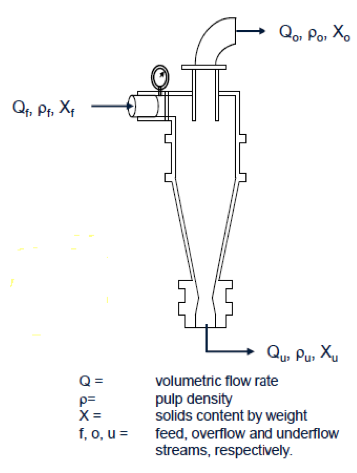
Contents Objectives Upon completing this lesson students should be able to: Explain the method used to assess the performance of separators. Illustrate partition analysis for comminution circuit. Analyze different types of partition curves. Explain the methods to access separation efficiency from partition curve. Reading & Lecture If ideal, […]
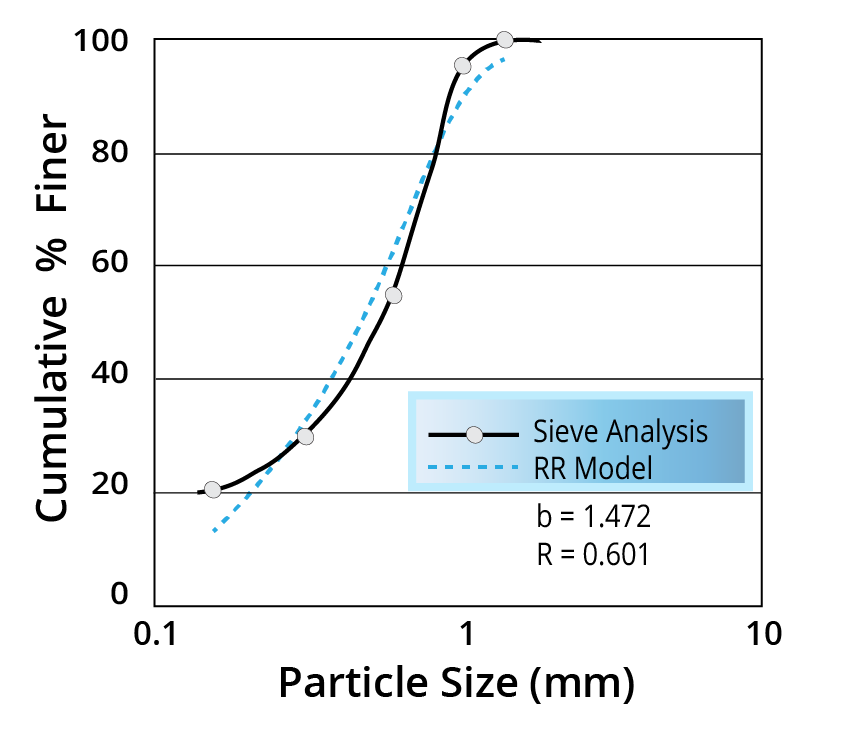
Contents Objectives After completing this lesson students should be able to: Demonstrate understanding of various method involved in measuring particle size. Explain the importance of particle size analysis and its application. Differentiate between the different models used for predicting particle size. Explain the different convention followed in measuring particle size. […]
Contents Introduction Introductory narrative or video Objectives Upon completion of this lesson students should be able to: Differentiate between different type metallurgical accounting methods and benefit of metallurgical accounting. Recall the definitions of grade, recovery, yield and other characteristics used in mass balancing. Recognize the application of two product formula […]
Introduction Insert intro narrative or video. Objectives By the end of this lesson students should be able to: Explain the role of Extractive Metallurgy and its sub disciplines in mining industry. Explain mineral processing and processes involved. Distinguish between ore, mineral and rocks. List different physical properties of ore and […]
COURSE INFORMATION Title: Introduction to Mining Systems and Equipment Department/Number: AMIT 135 Credits: 4 Prerequisites: N/A Location: Fairbanks Pipeline Training Center (FPTC) Room #2 Meeting Dates/Time: TBD INSTRUCTOR INFORMATION Name: Tathagata Ghosh, Aibyek Khamkhash Office Location: 317 Duckering Building, University of Alaska Fairbanks Office Hours: by Appointment Telephone/Email: 907-474-6917 […]