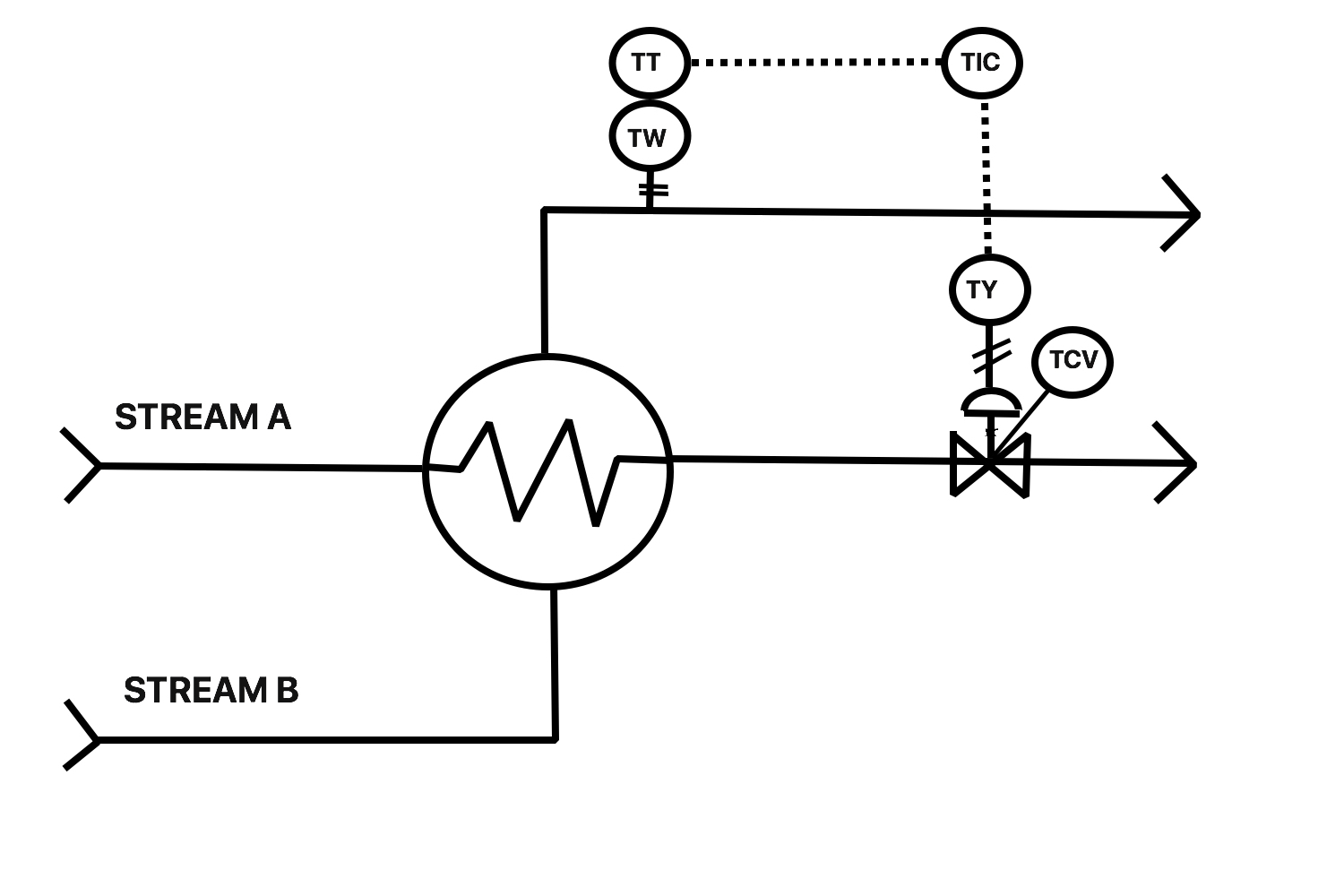
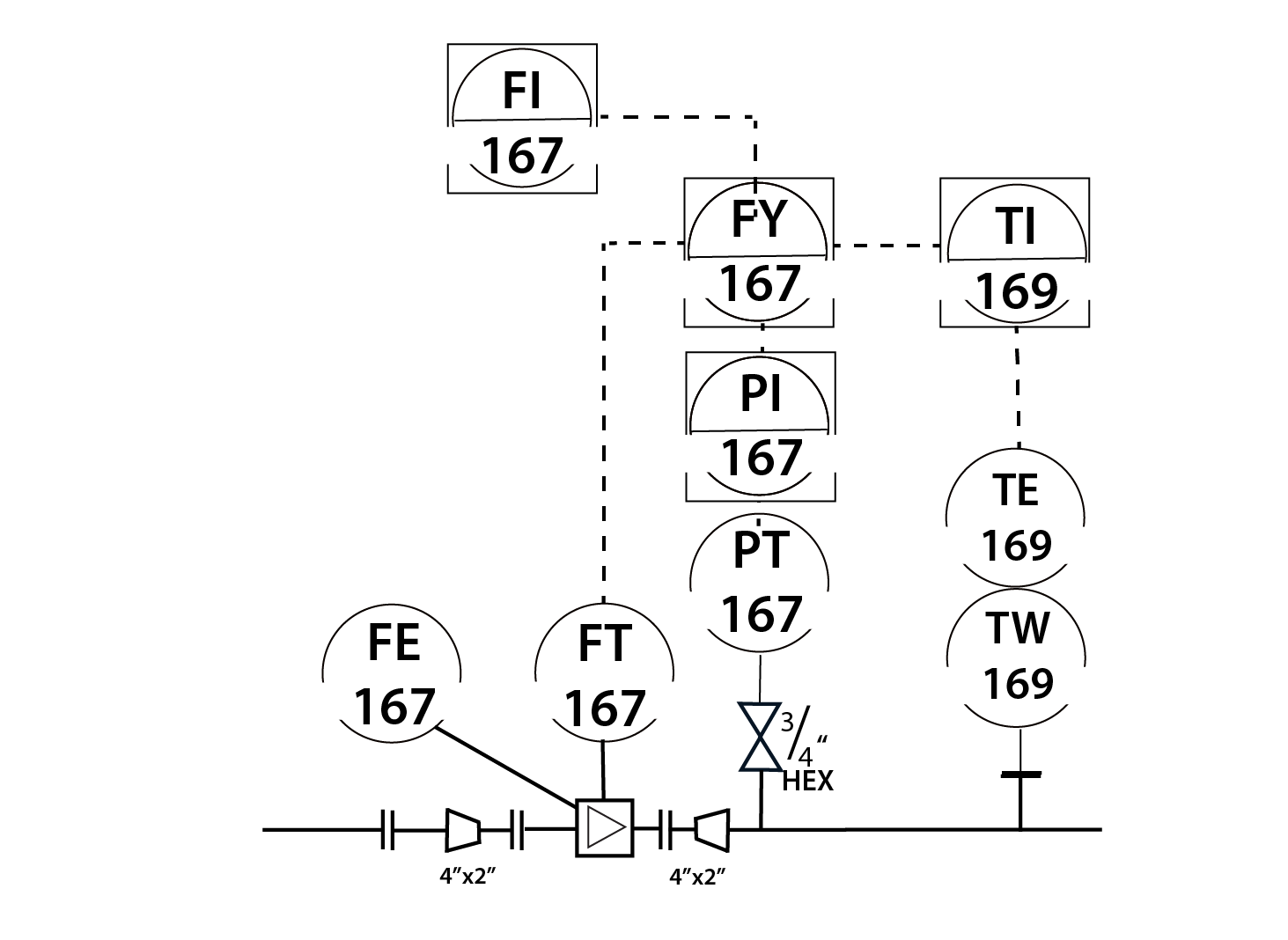
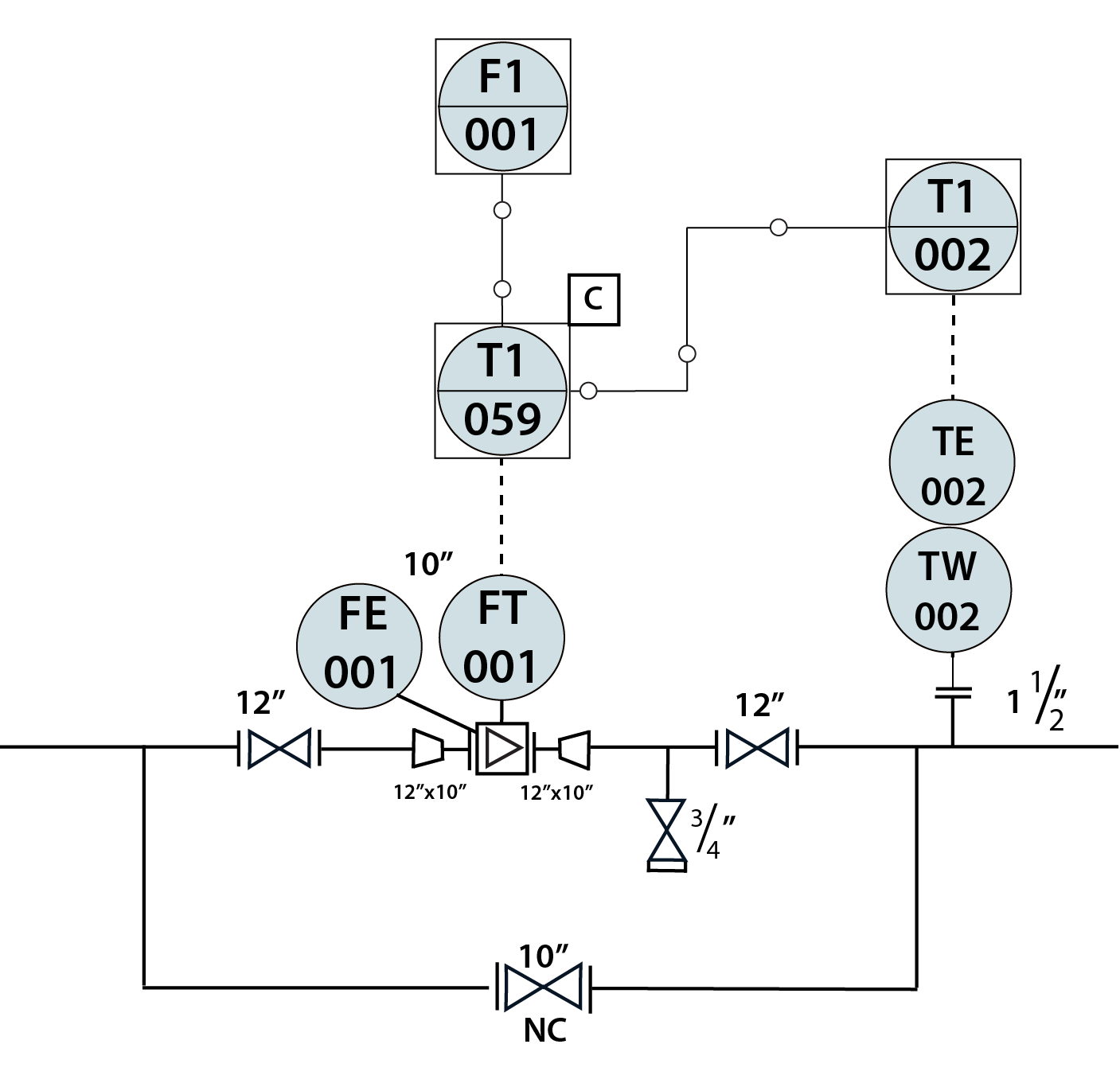
Objectives Review Different Types of Drawings Identify instrumentation on a P&ID, using the symbols from Chapter 12 Describe a control loop and its function, based on a P&ID layout Reading
PRT F140
14 posts
Contents Objectives Identify components of control valves and regulators Describe various operating scenarios Discuss valve actuators and positioners Explain the ways to reverse controller output signals, and need for such changes Describe types of pressure regulator devices Reading Terms to Know Actuator, Valve Plug, Valve Assembly Valve positioner Sliding Stem […]
Objectives Define basic controller terms — overview Outline the common controller settings Identify physical configurations for controllers Describe final control elements Identify components Identify applications Terms to Know Control valves: ATO, ATC Control Valve failure modes — FC, FO, Fail-Last Controller Action: Direct vs Reverse Local/Remote Controllers (location) Local/Remote Control/Setpoint […]
![A diagram of an I/P Transducer [140-10-01]](https://millops.community.uaf.edu/wp-content/uploads/sites/605/2017/03/millops-140-10-01.png)
Contents Objectives Describe the relationship between sensors, transducers, and transmitters in process control loops Compare and contrast the transmitter/transducer input and output signals Calculate: % span Scaling: Input to Output (linear) Review control loop function based on a process control scheme diagram Reading Terms to Know Discrete Sensing Element Integrally […]
Contents Objectives Describe Process Control Explain the function of a control loop Compare “Closed Loops’ and “Open Loops’ Identify the components of a control loop Describe signal transmission types Reading Terms to Know Setpoint Open Loop, Closed Loop, Feedback Control, Measure, Manipulate Sensor, Transmitter, Controller, Transducer, Final Control Element Live […]
Contents Objectives Discuss and identify major analytical instruments Discuss miscellaneous/specialty instruments Activity — PID/Instrument ID Test review Reading Terms to Know and Discuss Hand-Held, In-Line Visual, photometric pH, ORP, Conductivity Opacity, Turbidity Chromatograph, Spectrometer CEMS, personnel monitors Quantitative, Qualitative Rectilinear speed, Rotational speed Why Monitor Analytical Variables? Environmental Monitoring/Reporting Mechanical […]
Contents Objectives Define major terms associated with flow and flow measurement Identify common types of flow sensing and measuring devices Discuss and demonstrate the difference between total volume, flow rate, volumetric flow, mass flow Net and Gross Flow (temperature corrections) Review P&ID symbols for flow instrumentation Demonstrate relationship between dP […]
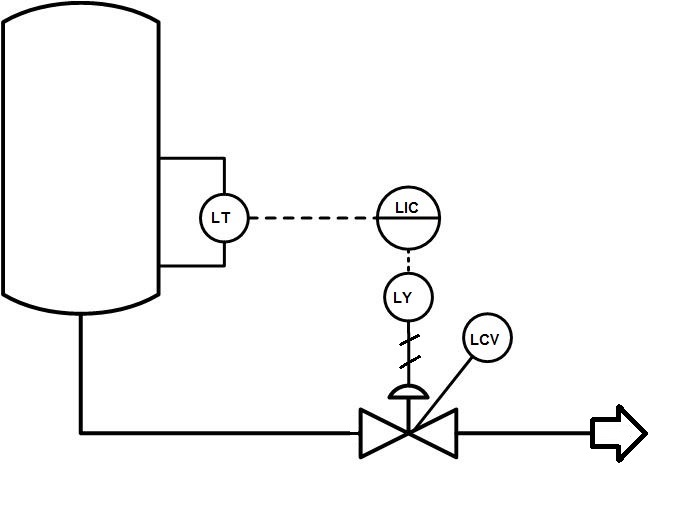
Contents Objectives Define ‘level’ and related terms Describe common types of Level instrumentation Demonstrate level measurements — bubbler, sight glass Perform level calculations and conversions Review Level instrumentation symbols on PID’s Perform pressure, temperature, level calculations – review Reading Innage/Ullage Question: Why might you use one or the other? Direct/Indirect […]
Contents Objectives Define ‘temperature’ and related terms Identify common types of Temperature instrumentation Perform temperature and pressure conversion calculations Review Temperature instrumentation symbols on PID’s Reading Temperature — Terms to Know Sensor — will respond to the process variable Temperature Heat Transfer, Conduction, Convection, Radiation Phase Change, Heat of Vaporization […]
Contents Objectives Define pressure and formula P=F/A Define terms associated with pressure and pressure instruments, per textbook Identify common types of pressure-sensing/measuring instruments used in the process industry: manometers pressure gauges differential pressure (d/p) cells strain gauge transducers (‘piezoelectric effect’) capacitance transducers Describe the purpose and operation of pressure instruments […]