AMIT 135: Lesson 2 Circuit Mass Balancing – Mining Mill Operator Training

Contents

Introduction

Introductory narrative or video

Objectives

Upon completion of this lesson students should be able to:

Differentiate between different type metallurgical accounting methods and benefit of metallurgical accounting.
Recall the definitions of grade, recovery, yield and other characteristics used in mass balancing.
Recognize the application of two product formula for balancing.
Provide a brief idea about multi component balancing for complex ores.

Reading

Mass and Volume Balancing

The most important rule governing the accounting of a processing plant or unit operation is that mass can be neither created nor destroyed.

Mass In = Mass Out

Volume In = Volume Out

Mass and Component Balance

Mass Component Balance — Outotec Concentrator

The component balance is true for any assay type such as any element content, % finer than, water-to-solids ratio etc.

Ff = Cc + Rr

Mass Yield or Mass Recovery

$\LARGE \mathbf{Mass\; Yield, Y = \frac{tons/hr\; Plant\; Concentrate}{tons/hr\; Plant\; Feed} = \frac{C}{F}}$

Two-Product Formula

Given the mass and component balance equations :

F = C + R

Ff = Cc + Rr

Mass yield (Y) can be solved as a function of the stream, assays which yields the two-product formula:

R = F- C

Ff = Cc + r (F – C)

$Mass Yield, Y = \frac{C}{F} = \frac{(f-r)}{c-r}$

Mass Yield Formula Example

$Mass Yield, Y = \frac{C}{F} = \frac{(f-r)}{c-r}$

$Mass Yield = \frac{(0.50 - 0.14)}{(24.5 - 0.14)}\ast 100$

Mass Yield = 1.5%

Component Recovery

In many mineral processing applications, the focus is to maintain maximum recovery of the valued mineral or element while also maximizing upgrade or concentrate assay.

$Component Recovery = \frac{Cc}{Ff} = \frac{c}{f} \ast \frac{(f-r)}{c-r} = \frac{c}{f}\ast Y$

Component Recovery Example

$Cu Recovery, R = Y\ast \frac{c}{f}$

$Cu Recovery, R = 1.5\ast \frac{(24.5)}{(0.50)}\ast 100$

Cu Recovery, R = 73.5%

Concentration Ratio, CR

$Concentration Ratio, CR = \frac{c}{f}$

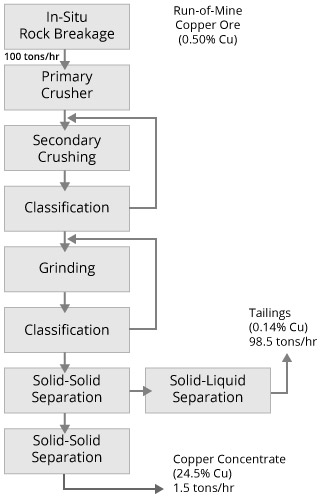
Complex Sulfide Ore Metallurgical Balance

Brunswick No.1 Concentrator

Process Stream	Weight (%)	Assays
Process Stream	Weight (%)	Pb%	Zn%	Cu%	Ag%
Mill Feed	100.00	3.21	7.93	0.33	2.26
Copper Concentrate	0.74	4.69	4.65	22.64	50.39
Lead Concentrate	4.80	42.20	9.62	0.33	15.48
Zinc Concentrate	10.52	1.12	57.76	0.18	1.75
Tailings	83.94	1.22	1.61	0.15	1.14
Metal Recovery (%)		63.1	76.6	50.9

Section	Process Stream	Mass Flow (tph)	Copper Assay (%)	Cu Recovery (%)
Complete Plant	Mill Feed	709	0.53	100
	Mill Concentrate	10	33.00	88.3
	Mill Tailings	699	0.06	11.7
Rougher	Feed	716	0.55
	Concentrate	28	12.00	83.6
	Tailings	688	0.09
Scavenger	Feed	253	0.13
	Concentrate	6	2.00	2.4
	Tailings	247	0.09
Cleaner	Feed	29	12.00
	Concentrate	15	22.00
	Tailings	14	1.30
Re-Cleaner	Feed	18	20.00
	Concentrate	11	31.00
	Tailings	7	3.00
Final Cleaner	Feed	11	31.00
	Concentrate	10	33.00	88.3
	Tailings	1	5.00

Mass/Volume Flow Determination

The relationship between the mass (M) and the volume flow (Q rates in a given stream is defined as: $M=\frac{Q\rho_{p} X}{100}$
$\rho_{p}$ = the pulp density (solids and water) in lbs/ft³X = solids concentration in % by weight
Volumetric flow rate can be measured by flow meters, P-Q curve relationships for pumps or directly measured.
Pulp density can be measured using a Marcy Density of nuclear density gauge.
The solids concentration can be estimated using a common expression or directly measured.

Pulp Density

Density (ρ) is the ratio of the mass weight (M) of a substance and the total volume (V):
$\rho = \frac{Mass}{Volume} = \frac{M}{V}$
Water has a density of:
- 1.0gm/ml or 1.0gm/cm³
- 1000kg/m³ – 1tonne/m³
- 62.4lbs/ft³
Specific gravity is the ratio of the material density over the density of water:
$sp.gr.=\frac{\rho }{\rho _{w}} = \frac{\rho }{62.4lb/ft^{3}}$

Marcy Scale

The Marcy scale is a common tool used in preparation plants to measure pulp density.
The scale uses a container that allows a volume of exactly 1000 ml.
After collecting the sample, the container is hung on a weight scale which measures in grams.
The printed scale reads the pulp density directly in grams/ 1ml.
Since water density is 1.0 gm/ml, the scale also indicates the specific gravity of the pulp.
$sp.gr.=\frac{\rho _{p}}{1.0gm/ml}$

Mass Flow Determination Example

A classifying cyclone is being fed slurry at a volumetric flow rate of 1000 gpm. The specific gravity of the slurry is 1.1 and the solids concentration was determined to be 15.0 °/o by weight. Determine the mass feed flow rate in tons per hour:

$M=\frac{Q\rho _{p}X}{100}$

$M=\frac{(Q gal/min)(0.13368ft^{3}/gal)(sp.gr.)(62.4lb/ft^{3})(X)(60min/hr)}{(2000lbs/ton)(100)}$

$M=\frac{(Q\rho _{p}X)(sp.gr.)(X)}{(4)(100)}$

Solution:

$M (tph) = \frac{(100 gal/min)(1.1)(15.0)}{(4)(100)}=41.3 tph$

Volumetric Balancing Using Pulp Density

Pulp density measurements around unit operations such as dense medium separators and classifying, cyclones can be used to assess volume yield.
Consider the balance around a classifying cyclone: $Q_{f}=Q_{u}+Q_{o}$
$Q_{f}\rho _{f}=Q_{u}\rho _{u}+Q_{o}\rho _{o}$
$since (Qvol/time)\ast (\rho\: mass/volume)= Pulp\: mass/time$
Thus, the volumetric yield to the underflow stream can be obtained from the following expression: $Volume\: Yield\: to\: Underflow=\frac{Q_{u}}{Q_{f}}=\frac{(\rho _{f}-\rho _{o})}{(\rho_{u}-\rho _{o})}\times 100$

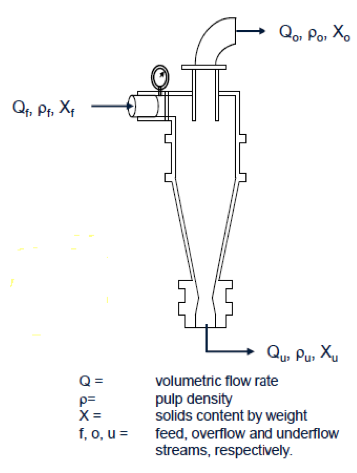
A diagram depicting formulas for figuring the balance around a classifying cyclone — Formulas for figuring the balance around a classifying cyclone
[diagram 135-2-1]

Slurry Solids Concentration by Weight

A classifying cyclone is treating 150 gallons/min of slurry. A plant technician has measured the pulp densities of the process streams using a Marcy density gauge and reported the following: Ïf = 1.08 gm/ml, Ïo = 1.03 gm/ml and Ïu = 1.20 gm/ml. Determine the volumetric flow rates to each stream.

Solution:

$Y_{u}=\frac{(\rho_{f}-\rho _{o})}{(\rho _{u}-\rho _{o})}\times 100=$ _________%

$Q_{u}=Q_{f}Y_{u}=150 \times$ _________ = _________ gallons/min

$Q_{o}=150-$ _________ = 150 X (1 – _________) = __________ gallons/min

The solids concentration X of a slurry by weight can be measured directly by:
- Collecting a sample,
- Measuring the weight of the total slurry or pulp M_p
- Drying the sample and
- Measuring the dry weight of solids M_s
  $X=\frac{M_{s}}{M_{p}}\times100= \frac{M_{s}}{M_{s}+M_{w}}\times 100$ M_w = water weight
This equation is often used to determine the amount of water in a process stream1 knowing the solids concentration by weight and the tons/hr of solids in a process stream.
$M_{w}\frac{M_{s}}{X}-M_{s}$

Solids Concentration Example

The underflow stream from the classifying cyclone bank contains 100 tons/hour of ore which represents 45% of the total slurry mass.

The downstream concentrators require a feed solids concentration of 30% by weight. How much water is required to be added to dilute the stream to the required solids concentration?

Solution:

$Water in Cyclone Underflow = M_{w}=\frac{100tph}{0.45} - tph=$ ________ tph

$Water\: in\: Spiral\: Feed = M_{w} = \frac{100 tph}{0.30} - 100 tph =$ ________ tph

$Dilution\: Water\: Required = Q = \frac{(400)(m)}{(sp.gr.)(X)} = \frac{(400)(\; \; \; \; \; \; \; )}{(1)(100)} =$ ________ tph

= _______ gpm

% Solids & Pulp Density Relationship

It often occurs that the knowledge of the solids content is needed within a time frame less than the sample preparation and analysis time.
When this situation arises, the solids content by weight can be estimated knowing the pulp density (Ï_p =) as measured with the Marcy scale and using the following equation:
X% = $\frac{\rho _{s}(\rho _{p}-\rho _{w})}{\rho _{p}(\rho _{s}-\rho _{w})}\times 100$ Ï_s = solids density or specific gravity
â‰ˆ 2.65 for most host rock minerals.Ï_w = water density (62.4 lbs/ft³ or 1gm/ml) or specific gravity (=1).

Estimation of Solid Density

The density of solid can be estimated if you know the composition by weight or volume of each component in the solid and the respective solid densities.
For example, assume that raw ore is a two component system comprised of a valued mineral and host rock having relative densities of 6.30 and 2.65, respectively. The amount of valued mineral is 30% of the total ore.Total Solid Mass, M: Mineral + Host Rock – 30 + 70 = 100
Total Volume, Vs: ${\color{Red} \frac{M_{M}}{\rho_{M}}+\frac{M_{HR}}{\rho _{HR}} = \frac{30}{6.30}+\frac{70}{2.65}= 31.18}$
Total Solid Relative Density ${\color{Red} =\frac{M_{s}}{V_{s}} - \frac{100}{31.18} = 3.21}$

Circuit Balancing

The data generated from process units and circuits are used to make important decisions.
- Plant design considerations
- Operational efficiencies
- Potential upgrades
As such, reliable data is very important for an operating plant.
All data must be checked for proper balancing based on the ‘laws of conservation’.
‘What goes in’ = ‘What goes out’

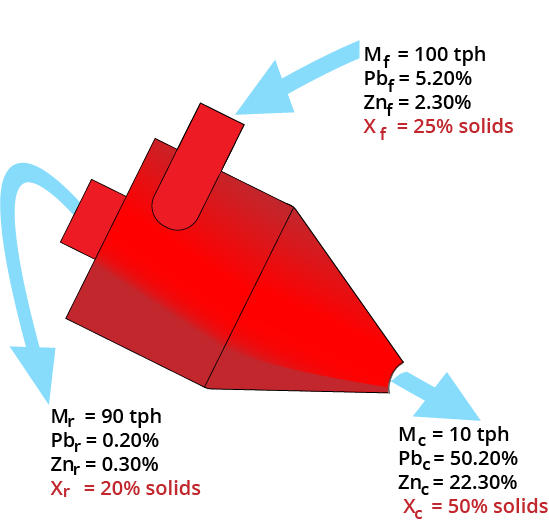
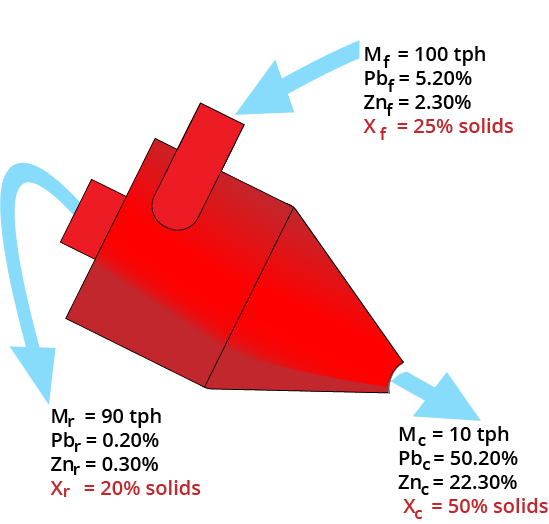
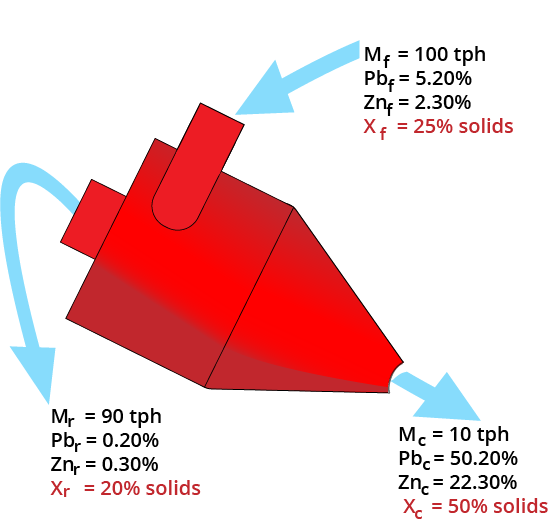
Material Balancing

Balance Summary
Overall: F = C+R

Pb: Ff₁ = Cc₁ + Rr₁
Zn: Ff₂ = Cc₂ + Rr₂
L/S Ratio: Ff₃ = Cc₃ + Rr₃

Questions:

Is this a good set of data?
Which values are not reliable?

Material Balance

Overall Balance

F = C+R

100 = 90 + 10

100 = 100

Lead Balance

Ff = Cc+ Rr

100(5.20) = 90(0.20) + 10 (50.20)

520.00=18.00 + 502.00

520.00= 520.00

Zinc Balance

Ff = Cc+ Rr

100(2.30) = 90(0.30) + 10 (22.30)

230.00= 27.00+223.00

230.00 â‰ 250.00

Slurry Balance

Mass balance equations must be satisfied!

Must use 1/Solids%

Product Stream	Mass (tph)	Solids (%)	Inverse Solids	Slurry (tph)
Clean	10	50	1/0.5	20
Reject	90	20	1/0.2	450
Feed	100	25	1/0.25	400

Water Balance

L/S Ratio Balance

Ff = Cc+ Rr

100(3.0) = 90(4.0) + 10(1.0)

300= 360+10

300 â‰ 370

Example: 3.0 = 3 parts Water to 1 part Solids = 25%

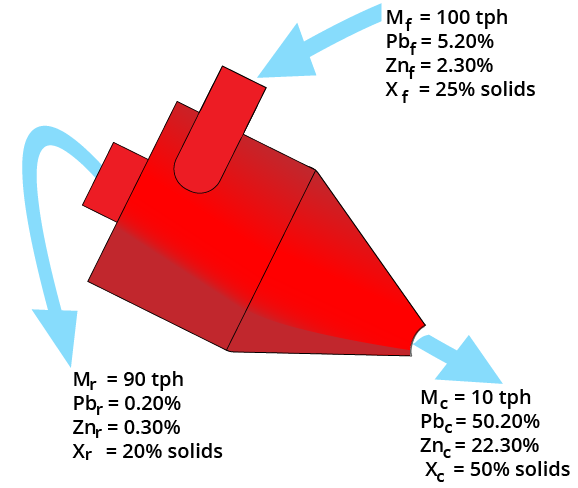
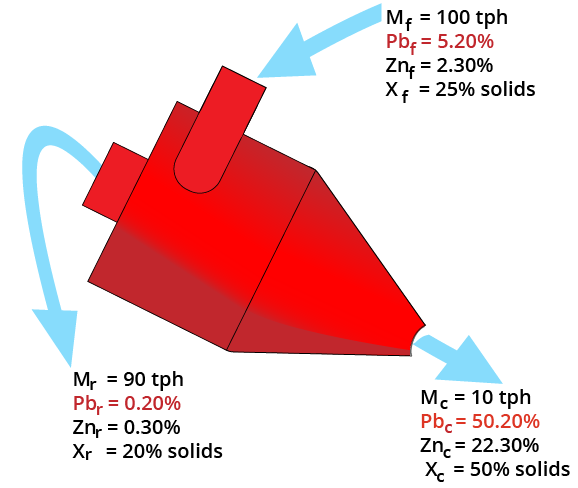
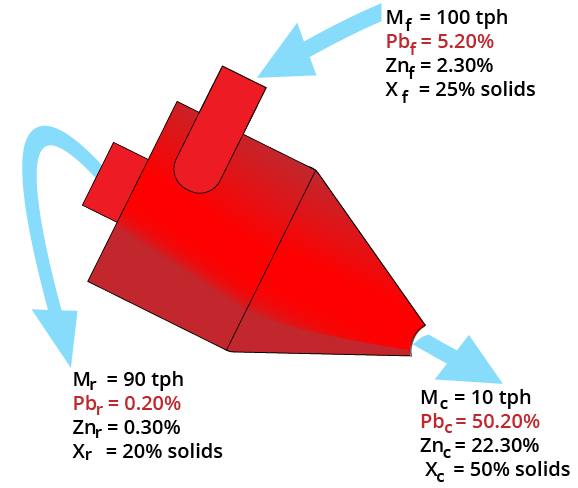
Two-Product Formula

Balances:

F = C + R

Ff = Cc + Rr

Multiply by r:

Ff = Cc + Rr

-(Ff = Cc + Rr)

______________

Ff- Ff = Cr – Cc

Rearrange:

F (r-f) = C (c-r)

Yield = C/F = (r-f) / (r-c)

* Only assays needed to get product-to- feed ratio

Two-Product Formula (Pb assays)

Overall:

C/F = 10/100

= 10%

Pb:

C/F=(5.20-0.20)/(50.20-0.20)

= 10%

Two-Product Formula Characteristics

Formula only applies under steady-state conditions

Formula very sensitive to variations in the reject assay, “r”

Formula inaccurate when component is not separated
Formula may calculate different yields for each assay (due to experimental errors)

Two-Product Formula (various assays)

Pb:

C/F = (5.2-0.2)/ (50.2-0.2)

= 10%

Zn:

C/F=(2.3-0.3)/(22.3-0.3)

= 9%

1/Solids:

C/F = (1/25-1/20) / ( 1/50-1/20)

= 33%

What to Do with Unbalanced Data

Eliminate Data

avoid collecting or ignore data that conflicts
most common approach in industry
arbitrary and highly subject to user biases
not getting full value out of your data

Adjust Data

create consistent balances by adjusting data
use method of “weighted least squares”
adjustments should (i) satisfy all mass balances equations and (ii) be as small as possible

Save