PRT 140: Lesson 4 Level – Mining Mill Operator Training

Contents

Objectives

Define ‘level’ and related terms
Describe common types of Level instrumentation
Demonstrate level measurements — bubbler, sight glass
Perform level calculations and conversions
Review Level instrumentation symbols on PID’s
Perform pressure, temperature, level calculations – review

Reading

Terms to Know

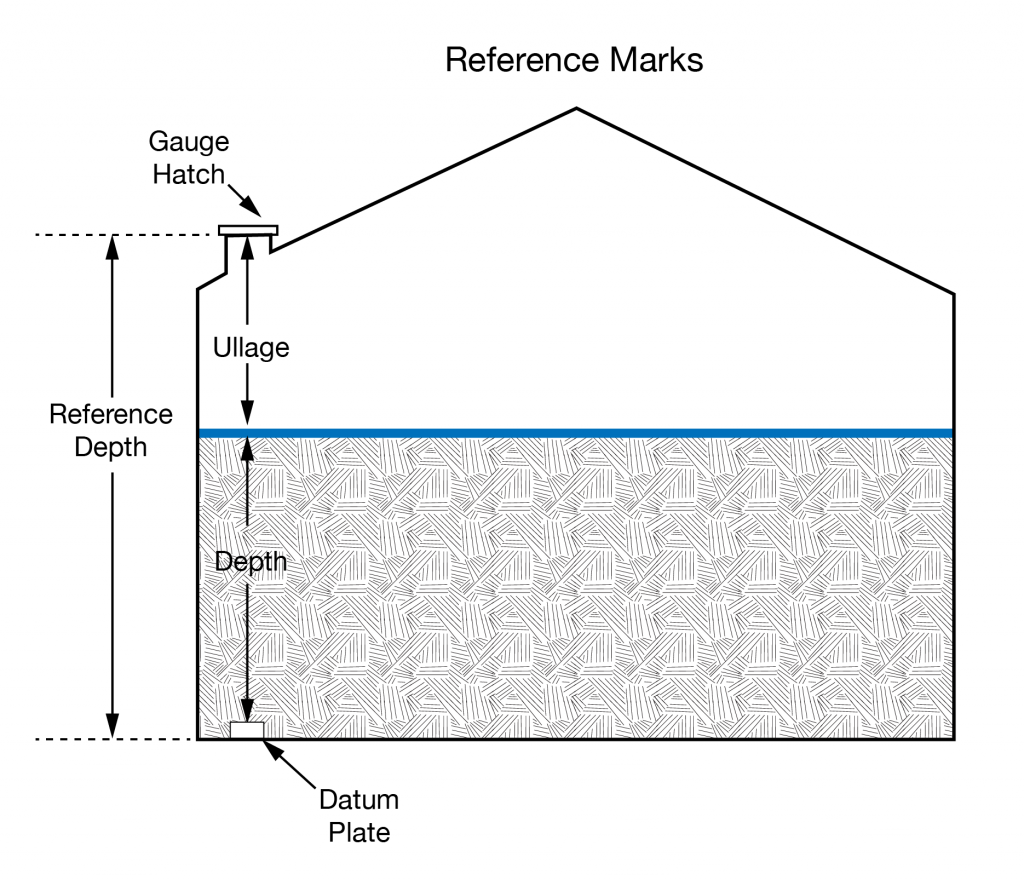
Innage
Outage/ullage
Direct level measurement
Indirect level measurement
Interface
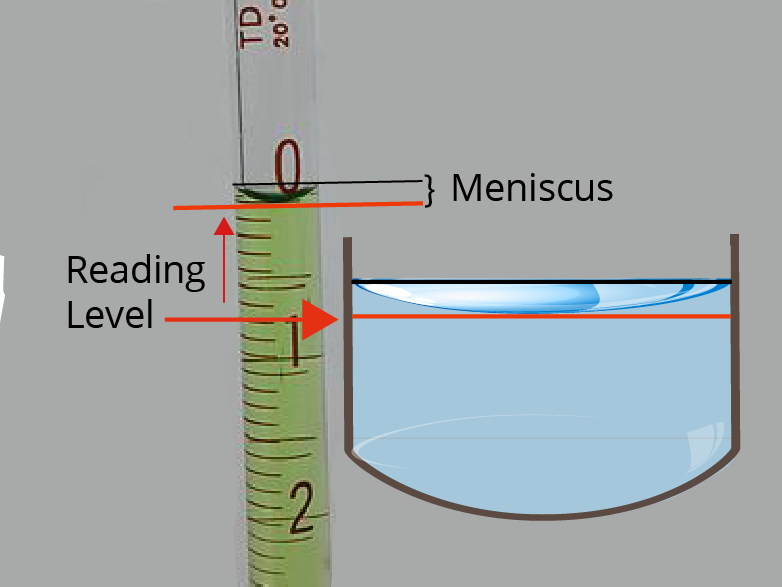
Meniscus
Hydrostatic Head Pressure
Level instruments, per presentation

Innage/Ullage

Question: Why might you use one or the other?

A diagram of fluid in a tank — Innage or Ullage
[image 140-4-01]

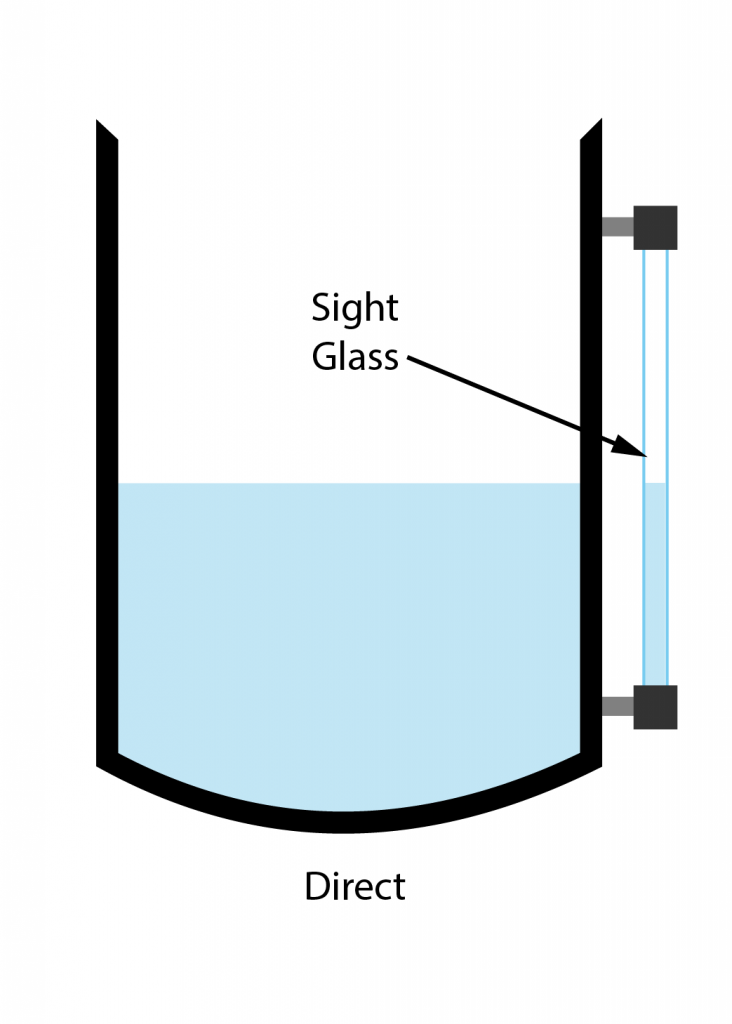
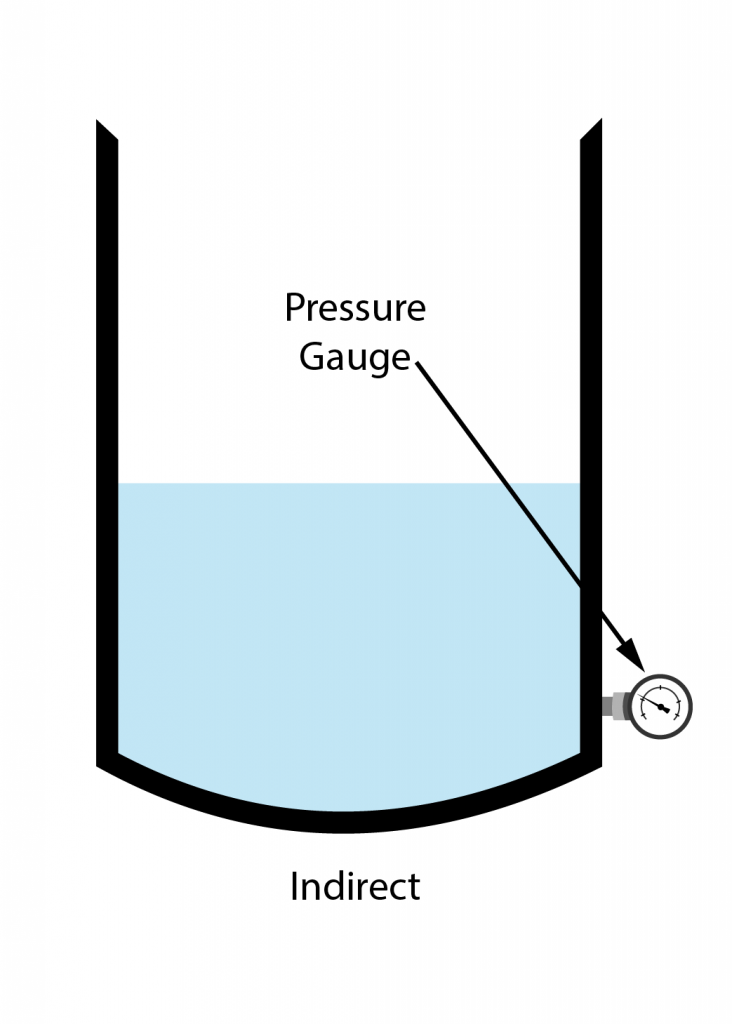
Direct/Indirect Level Measurement

Instrument directly reads the level

A diagram of a sight glass used for direct measurement — Direct Measurement
[image 140-4-02]

Instrument senses another property that is used to calculate level

A diagram of a pressure gauge to depict indirect measurement — Indirect Measurement
[image 140-4-03]

Direct/Indirect Examples

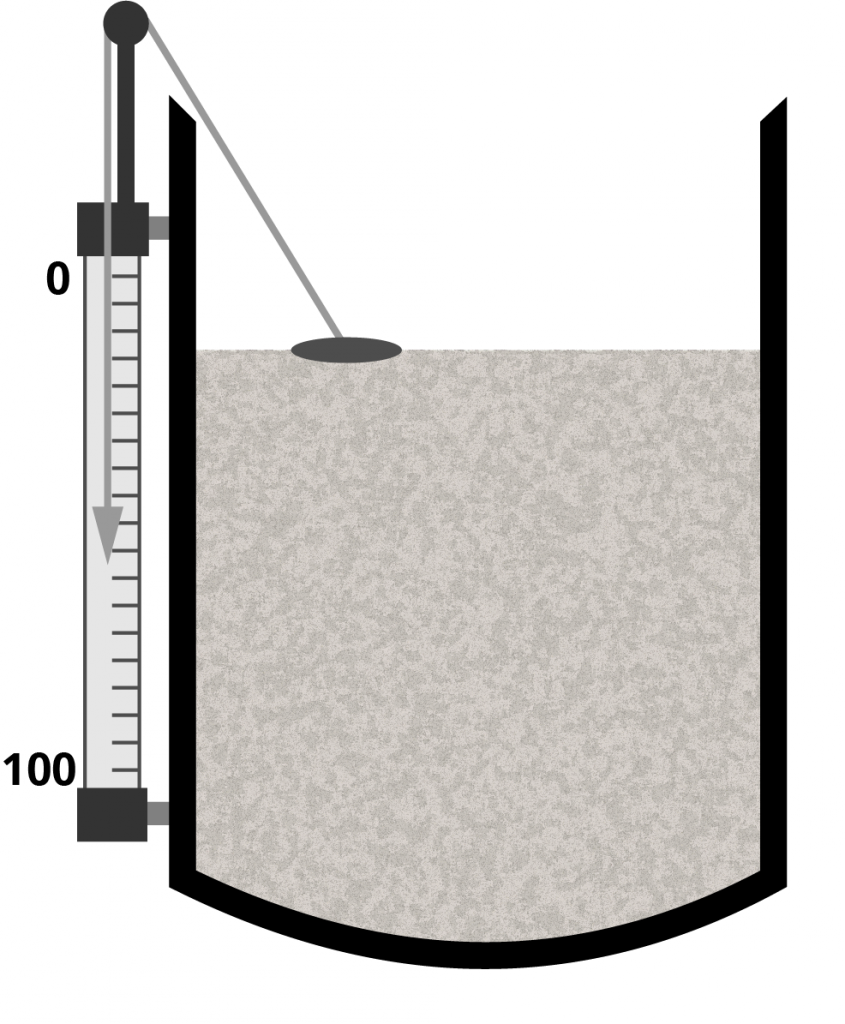
Direct Level Instruments

Sight glass
Float
Dipstick
Tape gauge

Indirect Level Instruments

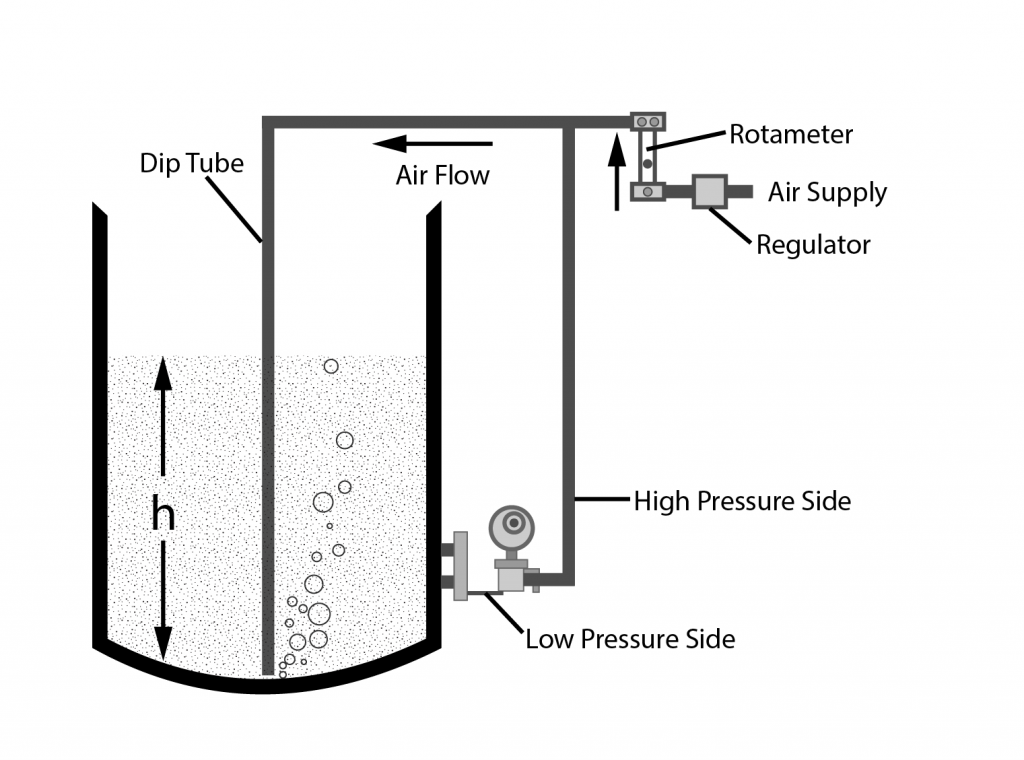
Bubbler
dP cells
Displacer

Interface / Meniscus

Interface

Meniscus

An image of a miniscus viewed through a pipette — An example of a meniscus
[image 140-4-05]

Level — Hydrostatic Head Pressure

Pressure exerted by the depth of the liquid column (we’ve looked at this before…)

P = (hydrostatic head pressure) = in. H2O

h = height of the liquid column (liquid level) = in.

SG = specific gravity of the liquid (water SG = 1)

P = (1 in wc) x (h in. ) x (SG)
in.

Or P = h x SG (if everything is in the right units)

UNITS of Level vs. Pressure

Units of level = a length, height measurement: ft, in, mm, etc.

Units of hydrostatic head pressure = length, height of a particular fluid:

in. H2O, mm Hg, in. w.c.,
Sometimes in ‘feet of head’, implying water (this is used for pump data, ref. PRT 130)

Example 1

An open tank contains a liquid with a specific gravity of 1.735. If the level of the liquid is 123 in., how much head pressure, in in. H₂O, will it exert?

A diagram illustrating h and PI for the example problem. — The open tank which contains a liquid, specific gravity 1.735
[image 140-4-07]

Equation to use:

P = (1 in. H₂O)(h)(SG) or P = h x SG
in.
SG = 1.735
h = 123 in.
P = (1 in. H₂O)(123 in.)(1.735)
in.
P = 213.4 in. H₂O

Level

If you know the hydrostatic head pressure and the SG, you can calculate level:

P = h x SG, so
h = P/SG
h is in.
P is in. H₂O

IMPORTANT: Data must be in the right units for this simple equation to work. Always verify units before using equations.

Example 2

An open top tank is filled with a liquid that has a specific gravity of 0.873. The liquid exerts a head pressure of 193 in. H₂O. What is the liquid level in inches?

P = (1 in. H₂O)(h)(SG) /in.
- P = 193 in. H₂O
- SG = 0.873
193 in. H₂O = (1 in. H₂O)(h)(0.873)/in.
h = (193 in.) / 0.873
h = 221.1 in.

Be very careful with units — this is not water, so giving a level height as in. H₂O makes no sense at all!

Level Instruments to Know

Sight Glasses
Float
Tape Gauge
dP cell
Bubbler
Displacer
Ultrasonic, Radar, Nuclear
Load Cells

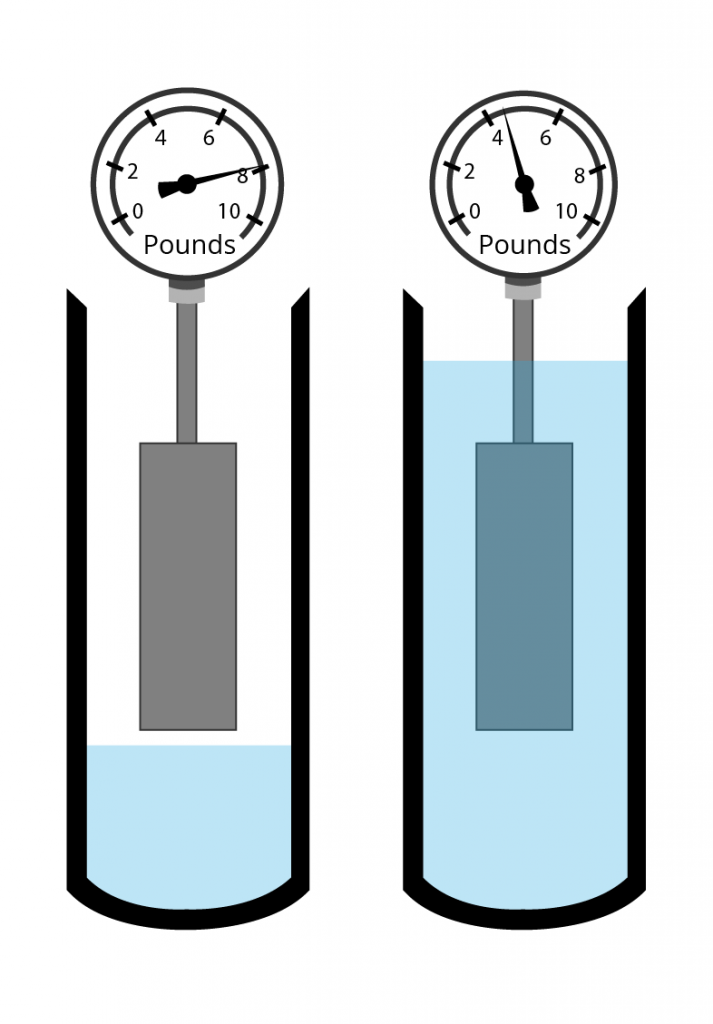
Direct Measuring Instruments

Sight Glass — see examples
Float
Gauge Tape

Direct measurement example — An example of a direct measure instrument.
[image 140-4-06]

dP vs. PI

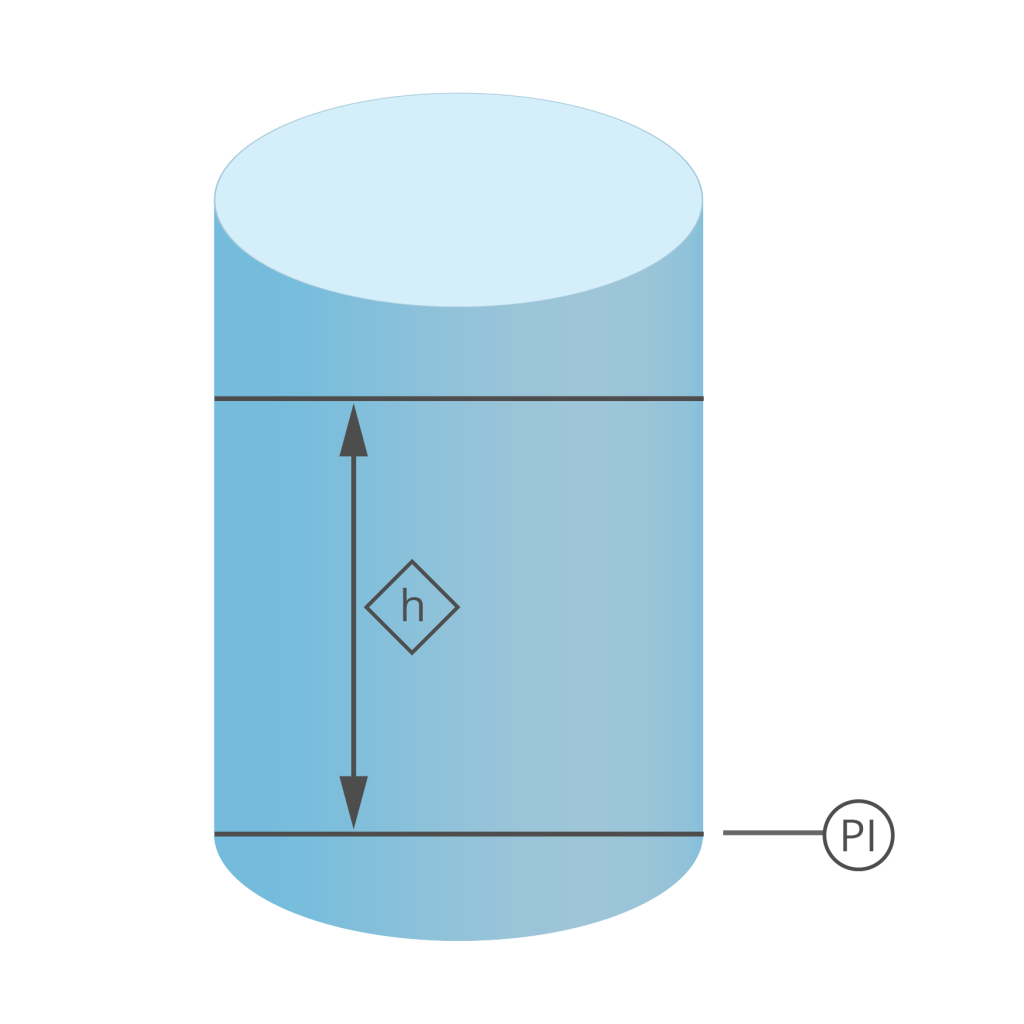
A diagram depicting how dP differs from PI — dP vs. PI
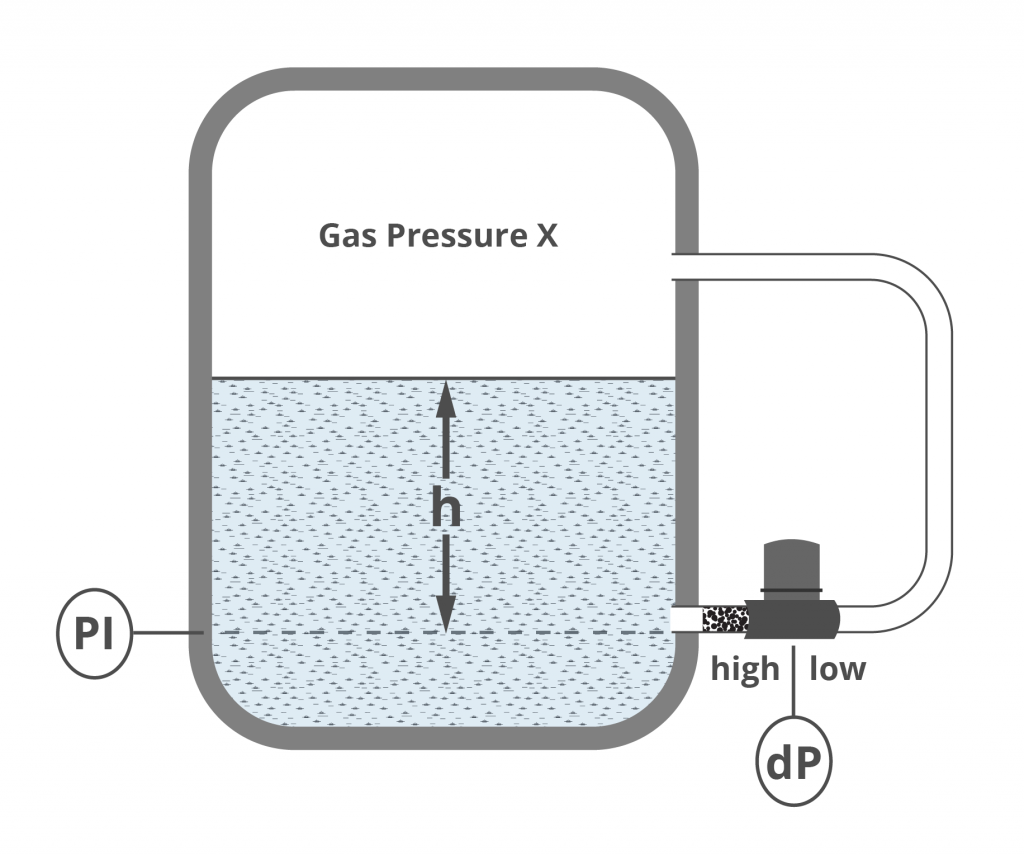
[image 140-5-06]

PI Measures All Pressures

PI measures P_X (vessel P) + P_H (hydrostatic)
P = P_X + P_H
P_X = 5 psi
P_H= h x SG = 67 in. x 1 = 67 in. H₂O
- 67 in. H₂O = 2.42 psi — (how do we know this?)
P = 5 psi + 2.42 psi
P = 7.42 psi at the PI

dP Cell – Measures Level Regardless of Vessel Pressure

Low side of dP measures P_X, vessel pressure
High side of dP measures P_X + P_H (hydrostatic)
Since it’s a differential, the final reading is
dP = (P_X + P_H) — P_X
dP = P_H
P_H = h x SG
P_H= h x SG = 67 in. x 1 = 67 in. H₂O
- 67 in. H₂O = 2.42 psi
dP = 2.42 psi

Advantage of dP Cell?

dP cell measures only the hydrostatic head from the liquid level — the vessel/system pressures are canceled out.
To use a single PI, you have to KNOW the vessel pressure and include that in any calculations.
Consider how the reading on the PI will change with vessel pressure — how do you know the level is changing or not?

Level — Bubbler

A diagram of a bubbler with labeled components — A diagram of a bubbler
[image 140-4-08]

What is the pressure at the bottom of the dip tube?
What is the formula for the pressure at the bottom of the liquid level, h?
P = h x SG

Example Question

What is the water height in inches, h, if the pressure on the bubbler reads:

1.5 psi
13 psi
72 psi

0.433 psi = 1 ft water (WHERE DOES THIS COME FROM?)

0.433 psi = 12 in. water (because 1 ft = 12 in.)

1 psi = 12 in. water/0.433

1 psi = 27.7 in. water

Bubbler P = h x SG, so P/SG = h

FIRST — convert all pressures to in. water

P = 1.5 psi = 41.6 in. H₂O
P = 13 psi = 360.1 in. H₂O
P = 72 psi = 1994.4 in. H₂O
- h = P/SG (SG =1.3)
h = 41.6/1.3 = 32 in.
h = 360.1 / 1.3 = 277 in.
h = 1994.4 / 1.3 = 1534.15 in.

(NOTE that the level units are different from P units)

How to Recognize Level Instruments in the Field

Many dP and P instruments are used to indirectly measure level. How do you identify them in the field?

Look at how they are connected/configured in the process.
Single PT — would have to be at the bottom of a liquid column, right? (not too commonly used this way)
dP is very common
First — make sure it’s a dP transmitter — H/L connections, possibly two visible leads to process
- One at bottom of a liquid column, one to atmosphere
- One at bottom of a vessel, one in the vapor space of a vessel
- Two connections to a liquid-full container, at a specific height differential
- One to a bubbler line, one to atmosphere
- Probably many more

The bottom line is — look at how it’s configured, think what information you get from that data

Displacers

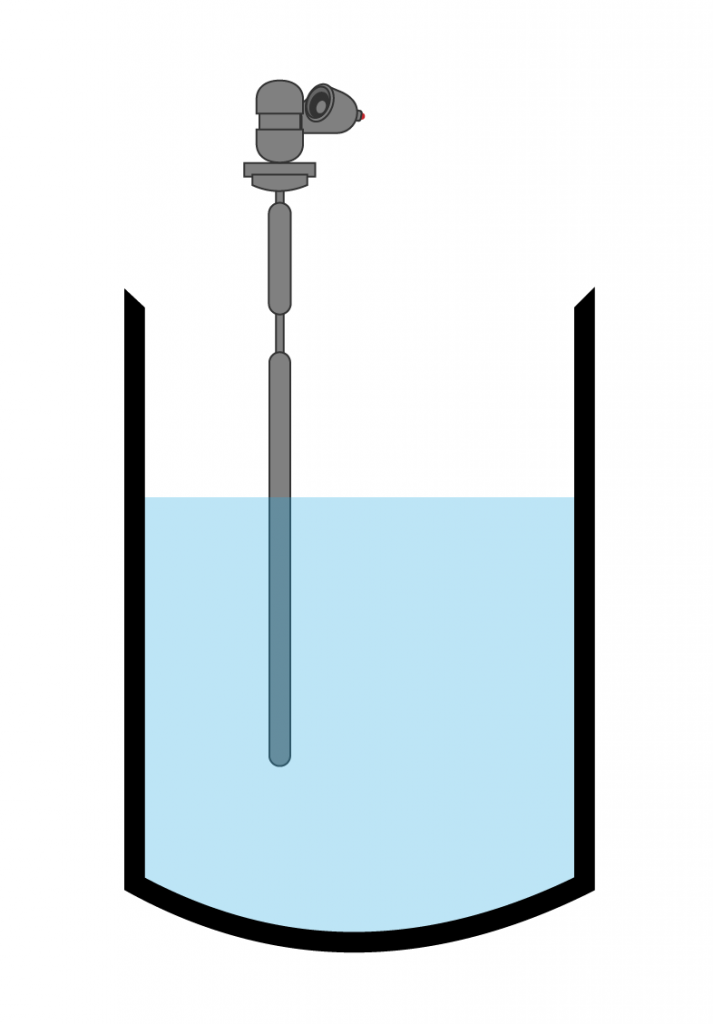
A diagram of a displacer — A displacer
[image 14-4-09]

A diagram illustrating buoyancy measured in pounds — Buoyancy reading
[image 140-4-10]

Other

Ultrasonic/Radar: Measure ullage distance, infers level. Used when physical sensors may not work (i.e. asphalt tankage)

Nuclear: uses gamma radiation to detect matter inside the vessel. Used for difficult measuring situations, extreme conditions

Load Cells: Weigh the contents, can calculate level

What other info do you need to make this calculation?

Level – PID Symbols

An example diagram with PIDs — PID symbols
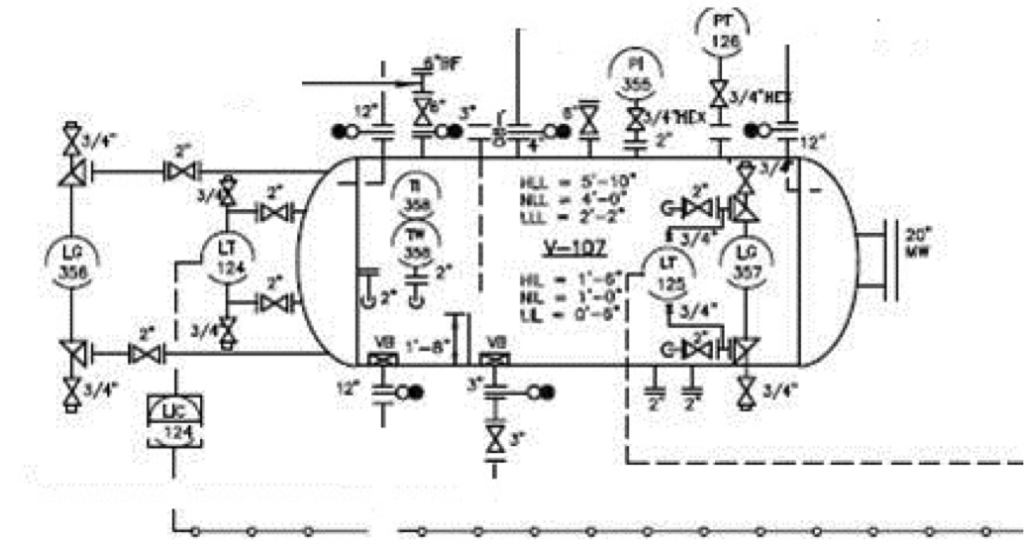
[image 140-4-11]

Review

In a closed container,

P₁V₁/T₁ = P₂V₂/T₂

Pressure and Temperature must be in ABSOLUTE UNITS —

P = psia
T = K or R

Volume units just have to be consistent

Step 1 = get all units and variables identified

450 psig, 125 C, 437 ft³ = 235 psig, 564ft³, ???C

Variables	Data, units
P₁	450 psig
T₁	125 C
V₁	437 ft³
P₂	235 psig
T₂	?
V₂	564 ft³

Step 2 = get all units correct (absolute T, P)

Variables	Data, units	Data, in absolute units
P₁	450 psig	464.7 psia
T₁	125 C	398 K
V₁	437 ft³	437 ft³
P₂	235 psig	249.7 psia
T₂	?	?
V₂	564 ft³	564 ft³

Step 3, set up and solve equations

(464.7 psia x 437 ft³) / 398 K = (249.7 psia x 564 ft³) / T₂

T₂ = (249.7 psia x 564 ft³ x 398 K) / (464.7 psia x 437 ft³)

T₂ = 276 K

T₂ = 3 C (answer should be in same units as original data, unless specified otherwise)

Scaling Calculations

Level instrument operating range is
5 ft — 85 ft. What is the 4-20 mA reading at different levels?

VALUE_B = {[(VALUE_A — LRV_A)/SPAN_A] x SPAN_B} + LRV_B

Level: LRV = 5 ft URV = 85 ft Span = 80 ft

Signal: LRV = 4 mA URV = 20 mA Span = 16 mA

So:

?? mA = {[(Level Reading — 5 ft)/80 ft] x 16 mA} + 4 mA