Mining Mill Operator Training
Occupational Endorsement Program
Mining Mill Operator Training

PRT 140: Lesson 3 Temperature

Contents

Objectives

  • Define ‘temperature’ and related terms
  • Identify common types of Temperature instrumentation
  • Perform temperature and pressure conversion calculations
  • Review Temperature instrumentation symbols on PID’s

Reading

Temperature — Terms to Know

  • Sensor — will respond to the process variable
  • Temperature
  • Heat Transfer, Conduction, Convection, Radiation
  • Phase Change, Heat of Vaporization
  • Latent Heat, Sensible Heat
  • BTU
  • Fahrenheit/Rankine; Celsius/Kelvin
  • Absolute Temperature

Heat Transfer Terms

Convection

  • Mixing two substances or direct contact with one substance (exhaust gases)
  • hot coffee and cold cream
  • Convection oven — blows hot air around food

Conduction

  • Contact through a solid — no mixing; indirect contact
  • Shell/tube heat exchangers
  • Pan on electric stove top — pan conducts heat from burner to food

Radiation

  • Electromagnetic waves — no contact
  • Sunshine, heat from woodstove, burner flames in furnace
  • Pan under a broiler — radiant heat from burner/flame onto food

Absolute Temp/Pressure

Absolute temperature — temperature scale where 0 = ‘absolute zero’ – the temperature where no more heat can be removed from a system. This corresponds to 0 K or -273.15 °C.     Theory — no more molecular movement.

Absolute pressure – pressure measured from 0 = full vacuum. 0 psia = full vacuum

Gauge pressure – pressure measured from 0 = current atmospheric pressure. 0 psig = atmospheric pressure

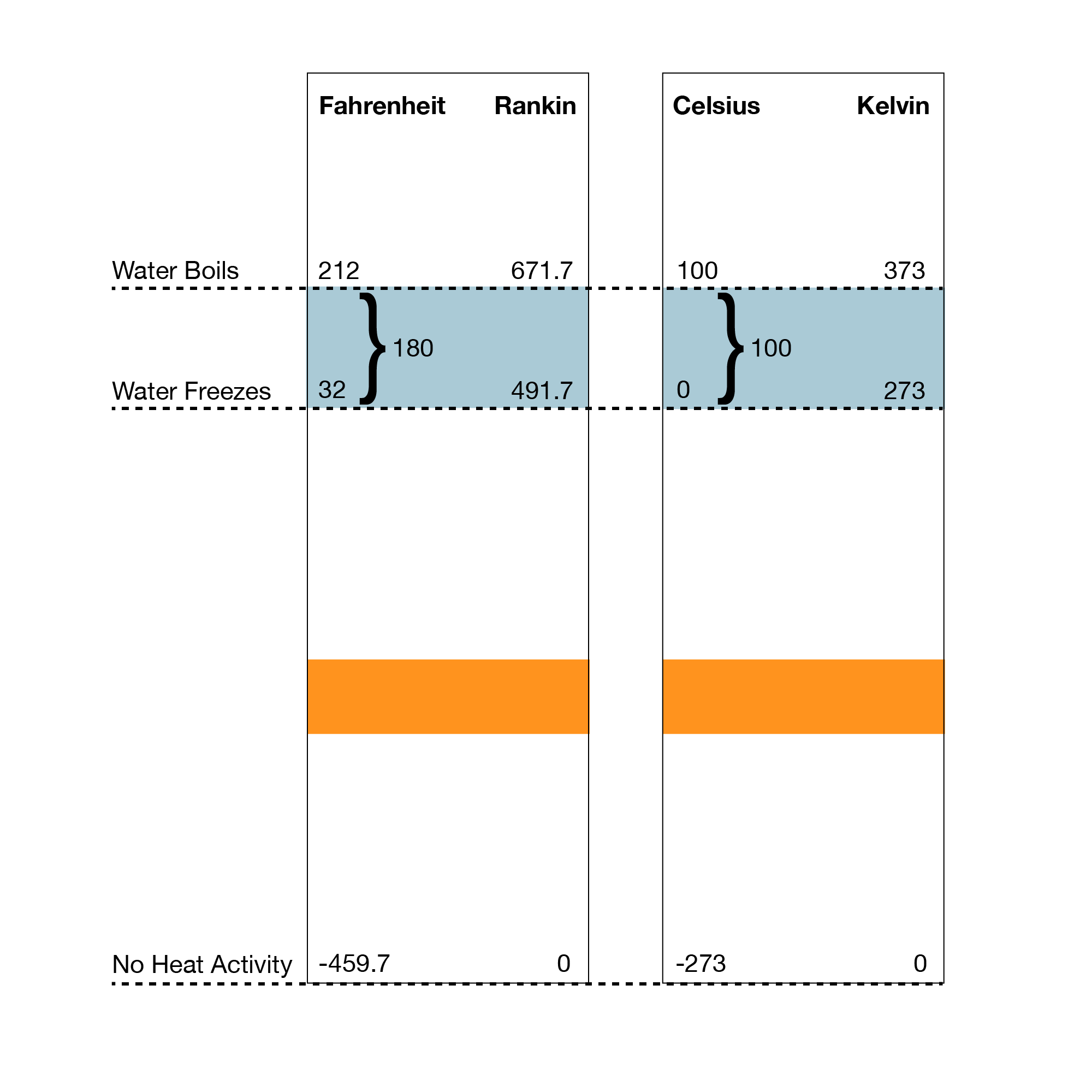
Temperature Scales vs. Actual Temperature

Absolute Temperature:

(Kelvin) K = C + 273

(Rankin) R = F + 460

F = (C x 9/5) + 32

C = (F-32) x 5/9

K = R x 5/9

R = K x 9/5

A diagram showing comparisons of temperature scales
Temperature Scales vs. Actual Temperature
[image 140-3-01-01]

Latent Heat vs Sensible Heat

  • Sensible Heat — heat that can be ‘sensed’ by a thermometer — i.e. the temperature changes
  • Latent Heat — heat that cannot be ‘sensed’ by a thermometer — i.e. temperature doesn’t change when phase is changing.
  • Boiling water stays at 212 F until all of it is steam — even while we keep adding heat. This is called the latent heat of vaporization.
  • Same idea when water freezes — releases latent heat.

Temperature Instruments

  • Thermowell
  • Thermometer
  • BiMetallic Strip
  • RTD — Resistance Temperature Device
  • Thermocouple
  • Thermistor
  • Temperature Gauge

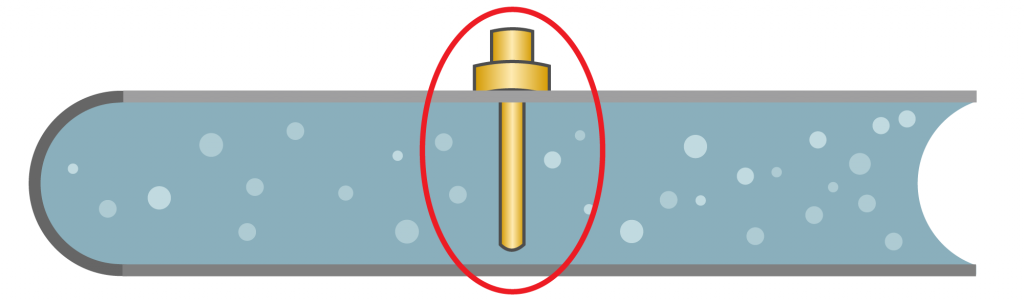
Thermowell

  • Not an instrument — it holds the instrument and protects it from the process, while allowing heat transfer
  • TW
A diagram of a thermowell
Thermowell
[image 140-3-02]

Thermometer

  • Glass Bulb — standard
  • Also IR — Infrared — non-contact
An infrared photo of a train in operation
Infrared Train, By Jagokogo (Own work) [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons
[image 140-3-03]

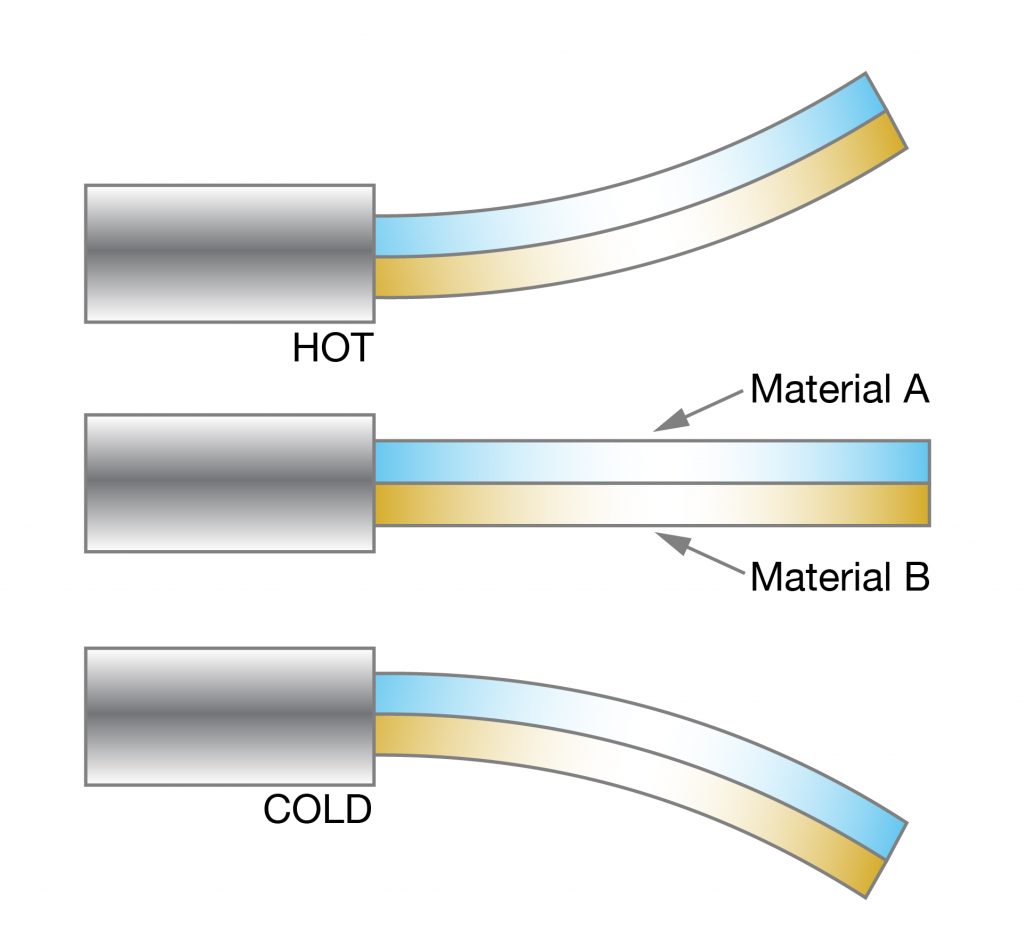
BiMetallic Strip

  • Two Dis-similar metals, bonded together
  • Expansion/Contraction with Temperature different for 2 metals
  • Movement of strip, moving temperature dial
  • Dial thermometer very common
A diagram of how bi-metalic strip reacts to templature.
Bi-metallic Strip
[image 140-3-04]

RTD — Resistance Temperature Device

  • Electrical resistance (ohms) will change with temperature — varying output signal
  • More accurate than Thermocouple
  • Smaller operating range (-200F to 900F)
  • Ohms resistance in the RTD correlates to temperature — see tables

100 (1000) Ohm Platinum RTD Resistance Chart
Generally RTDs are a 3- or 4- wire configuration — fine electrical wires

4-wire RTD
[Image 140-3-06]
A diagram showing typical RTD design
Typical RTD Design
[image 140-3-07]

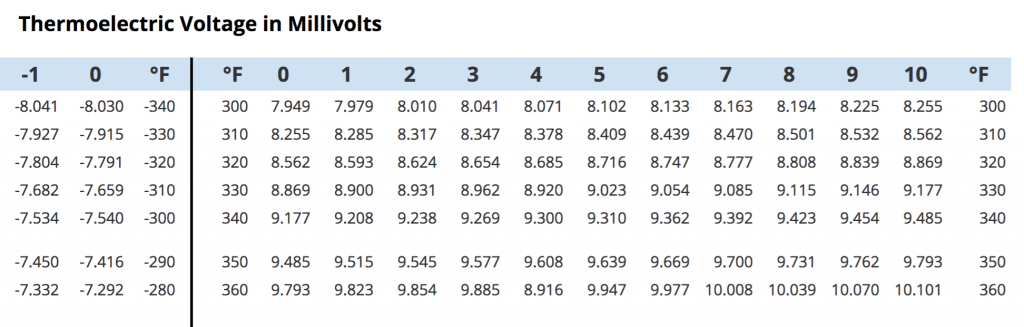
Thermocouple

  • Most common, simplest
  • Two dissimilar metals — generate voltage at their junction when they are heated.
  • Measured junction — connects to process
  • Cold junction/reference — connects to transmitter
  • mV generated across Thermocouple correlates to temperature — see tables
Thermocouple — excerpt from voltage chart
Thermocouple — excerpt from voltage chart
[image 140-3-08]

Thermocouples

  • Generally 2-wire configuration
  • Wires are thicker
  • made of the dissimilar metals
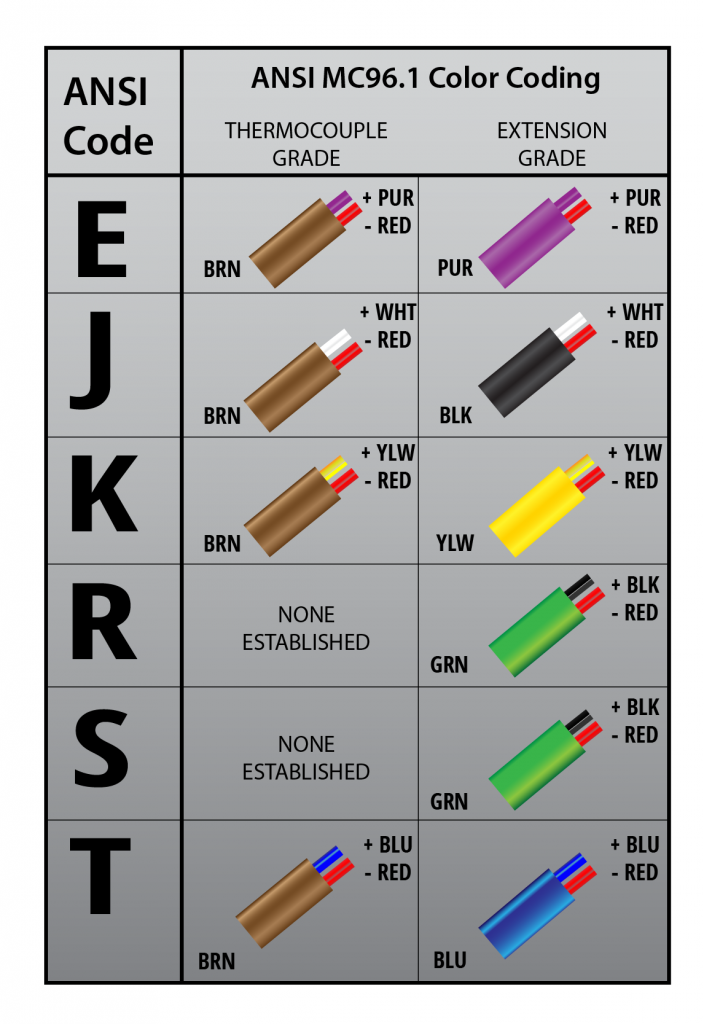
An image of a diagram of an ANSI MC96.1 Color Coding table
ANSI MC96.1 Color Coding table
[140-3-9]

Thermistor

  • Ceramic resistor — same principle as RTD —
  • Electrical resistance through thermistor changes with temperature
  • Usually small bead/disk
  • Registers very small temperature differences

Temperature Gauge

No transmitter — gauge face (like PI)

Standard Bi-Metallic Thermometer
[Image 140-03-11]

Temperature transmitters — How to identify them in the field

  • Read the nameplate on the instrument
  • Should include calibration range
  • Will include model number — can look it up
  • May include facility tag number
  • Look at how it’s connected to the process
  • Temperature sensors almost always have THERMOWELLS to house the sensor
  • Temperature sensors usually extend into the process stream — so there will NOT be an isolation valve on the process connection.

Temperature Conversion Calculations

  • Absolute: (Kelvin) K = C + 273
  • Absolute: (Rankine) R = F + 460
  • F = (C x 9/5) + 32
  • C = (F-32) x 5/9

Temperature Conversion

32 C = ?? F

F = (C x 9/5) +32

F = (32 x 9/5) + 32

F= 89.6

32 C = 89.6 F

25 F = ?? C

C = (F-32) x 5/9

C= (25-32) x 5/9

C= -3.9

25 F = -3.9 C

25 C = ?? F

F = (C x 9/5) +32

F = (25 x 9/5) + 32

F = 77

25 C = 77 F

100 C = ?? K

K = C + 273

K = 100 + 273

K = 373

100 C = 373 K

Temperature ‘linear scaling’ – NEW

The conversions between F and C temperature scales are an example of how we use the linear scaling calculation.

We looked at this equation in week 1 — it seems very complicated:

VALUEB = {[(VALUEA — LRVA)/SPANA] x SPANB} + LRVB

But it’s not, and you’ve been doing it already:

LRV = lower range value = the lowest value in the operating range

URV = upper range value = the highest value in the operating range

Span = URV — LRV

We pick two equivalent operating ranges:

Temperature — range from freezing to boiling:

F:   LRV=32 °F
URV=212 °F
Span = 180 °F
C:   LRV = 0 °C
URV = 100 °C
Span = 100 °C

Convert any C reading to F
(Whenever we get data, that set of units becomes the “A’ data)

F = {[(C reading — 0 C)/100 C] x 180 F} + 32 F

This equation is mathematically equivalent to:

F = (C X 9/5) + 32

Try it out! Convert 140 °C to F

F = {[(C reading — 0 C)/100 C] x 180 F} + 32F

F = {[(140C — 0C)/100C] x 180F} + 32 F

F = {[140C/100C] x 180 F} + 32 F

F = {1.4 x 180 F} + 32 F

F = 252 F + 32 F

F = 284 F

140 C = 284 F

F = (C X 9/5) + 32

F = (140 x 9/5)+32

F = (252) + 32

F = 284

 

 

140 C = 284 F

Linear Scaling Calculation
VALUEB = {[(VALUEA — LRVA)/SPANA] x SPANB} + LRVB

The linear scaling calculation is used to relate all kinds of linearly related scales. For example:

  • Operating temperature range will be 200 F to 600 F
  • We want the 4-20 mA signal from the transmitter to reflect that range.

We can use the scaling calc to calculate the mA reading at any temperature in the range — try 440 F.

F:   LRV=200 F   URV= 600 F   Span = 400 F

mA:   LRV = 4 mA   URV = 20 mA   Span = 16 mA

mA = {[(440F — 200F)/400F] x 16 mA} + 4 mA

mA = {[240F/400F] x 16 mA} + 4 mA

mA = {0.6 x 16mA} + 4 mA

mA = 9.6 mA + 4 mA = 13.6 mA at 440 F

Process Variable Relationships

Pressure, Volume, Temperature in a closed container

\frac{P_{1}V_{1}}{T_{1}} = \frac{P_{2}V_{2}}{T_{2}}

Pressure/Temperature are in Absolute Units

T = K,R         P = psia

V1, V2 both in the same units